If G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
To prove that AB2+BC2+CA2=3(GA2+GB2+GC2) for triangle ABC with centroid G, we will follow these steps:
Step 1: Define the vertices of the triangle
Let the vertices of triangle ABC be:
- A(B,C)
- B(0,0)
- C(A,0)
Step 2: Find the coordinates of the centroid G
The centroid G of triangle ABC is given by the formula:
G=(x1+x2+x33,y1+y2+y33)
Substituting the coordinates of A,B,C:
G=(B+0+A3,C+0+03)=(A+B3,C3)
Step 3: Calculate AB2,BC2,CA2
Using the distance formula d=√(x2−x1)2+(y2−y1)2, we find the squares of the lengths:
1. For AB2:
AB2=(B−0)2+(C−0)2=B2+C2
2. For BC2:
BC2=(0−A)2+(0−0)2=A2
3. For CA2:
CA2=(A−B)2+(0−C)2=(A−B)2+C2
Expanding this:
CA2=A2−2AB+B2+C2
Step 4: Combine AB2,BC2,CA2
Now, we combine these results:
AB2+BC2+CA2=(B2+C2)+A2+(A2−2AB+B2+C2)
Combining like terms:
=2A2+2B2+2C2−2AB
Step 5: Calculate GA2,GB2,GC2
Now we calculate the squares of the distances from the centroid G to each vertex:
1. For GA2:
GA2=(A+B3−B)2+(C3−C)2
Simplifying:
GA2=(A−2B3)2+(−2C3)2=(A−2B)2+4C29
2. For GB2:
GB2=(A+B3−0)2+(C3−0)2
Simplifying:
GB2=(A+B3)2+(C3)2=(A+B)2+C29
3. For GC2:
GC2=(A+B3−A)2+(C3−0)2
Simplifying:
GC2=(−2A+B3)2+(C3)2=(−2A+B)2+C29
Step 6: Combine GA2,GB2,GC2
Now we combine these results:
GA2+GB2+GC2=(A−2B)2+4C2+(A+B)2+C2+(−2A+B)2+C29
This simplifies to:
=(A2−4AB+4B2+4C2)+(A2+2AB+B2)+(4A2−4AB+B2)+3C29
Combining like terms gives:
=6A2+6B2+6C2−6AB9=2(A2+B2+C2−AB)3
Step 7: Final step
Now, we can multiply by 3:
3(GA2+GB2+GC2)=2(A2+B2+C2−AB)
Conclusion
Thus, we have shown:
AB2+BC2+CA2=3(GA2+GB2+GC2)
This completes the proof.
Let the vertices of triangle ABC be:
- A(B,C)
- B(0,0)
- C(A,0)
The centroid G of triangle ABC is given by the formula:
G=(x1+x2+x33,y1+y2+y33)
Substituting the coordinates of A,B,C:
G=(B+0+A3,C+0+03)=(A+B3,C3)
Using the distance formula d=√(x2−x1)2+(y2−y1)2, we find the squares of the lengths:
AB2=(B−0)2+(C−0)2=B2+C2
BC2=(0−A)2+(0−0)2=A2
CA2=(A−B)2+(0−C)2=(A−B)2+C2
Expanding this:
CA2=A2−2AB+B2+C2
Now, we combine these results:
AB2+BC2+CA2=(B2+C2)+A2+(A2−2AB+B2+C2)
Combining like terms:
=2A2+2B2+2C2−2AB
Now we calculate the squares of the distances from the centroid G to each vertex:
GA2=(A+B3−B)2+(C3−C)2
Simplifying:
GA2=(A−2B3)2+(−2C3)2=(A−2B)2+4C29
GB2=(A+B3−0)2+(C3−0)2
Simplifying:
GB2=(A+B3)2+(C3)2=(A+B)2+C29
GC2=(A+B3−A)2+(C3−0)2
Simplifying:
GC2=(−2A+B3)2+(C3)2=(−2A+B)2+C29
Now we combine these results:
GA2+GB2+GC2=(A−2B)2+4C2+(A+B)2+C2+(−2A+B)2+C29
This simplifies to:
=(A2−4AB+4B2+4C2)+(A2+2AB+B2)+(4A2−4AB+B2)+3C29
Combining like terms gives:
=6A2+6B2+6C2−6AB9=2(A2+B2+C2−AB)3
Now, we can multiply by 3:
3(GA2+GB2+GC2)=2(A2+B2+C2−AB)
Thus, we have shown:
AB2+BC2+CA2=3(GA2+GB2+GC2)
This completes the proof.
Topper's Solved these Questions
Similar Questions
AD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionIf G is the centroid of a ΔABC, then GA2+GB2+GC2 is equal to
View SolutionP and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
View Solutionlf G be the centroid of a triangle ABC and P be any other point in the plane prove that PA2+PB2+PC2=GA2+GB2+GC2+3GP2
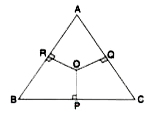
View SolutionIn the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB repectively of triangle ABC. Prove that :
AR2+BP2+CQ2=AQ2+CP2+BR2
View SolutionConstruct a triangle ABC given that :
BC = 4 . 5 cm, AB = 5 . 2 cm and CA = 3 . 8 cm
View SolutionIn a tetrahedron OABC, the edges are of lengths, |OA|=|BC|=a,|OB|=|AC|=b,|OC|=|AB|=c. Let G1andG2 be the centroids of the triangle ABC and AOC such that OG1⊥BG2, then the value of a2+c2b2 is
View SolutionIf G is the centroid of triangle with vertices A(a,0),B(−a,0) and C(b,c) then AB2+BC2+CA2GA2+GB2+GC2=
View Solution
