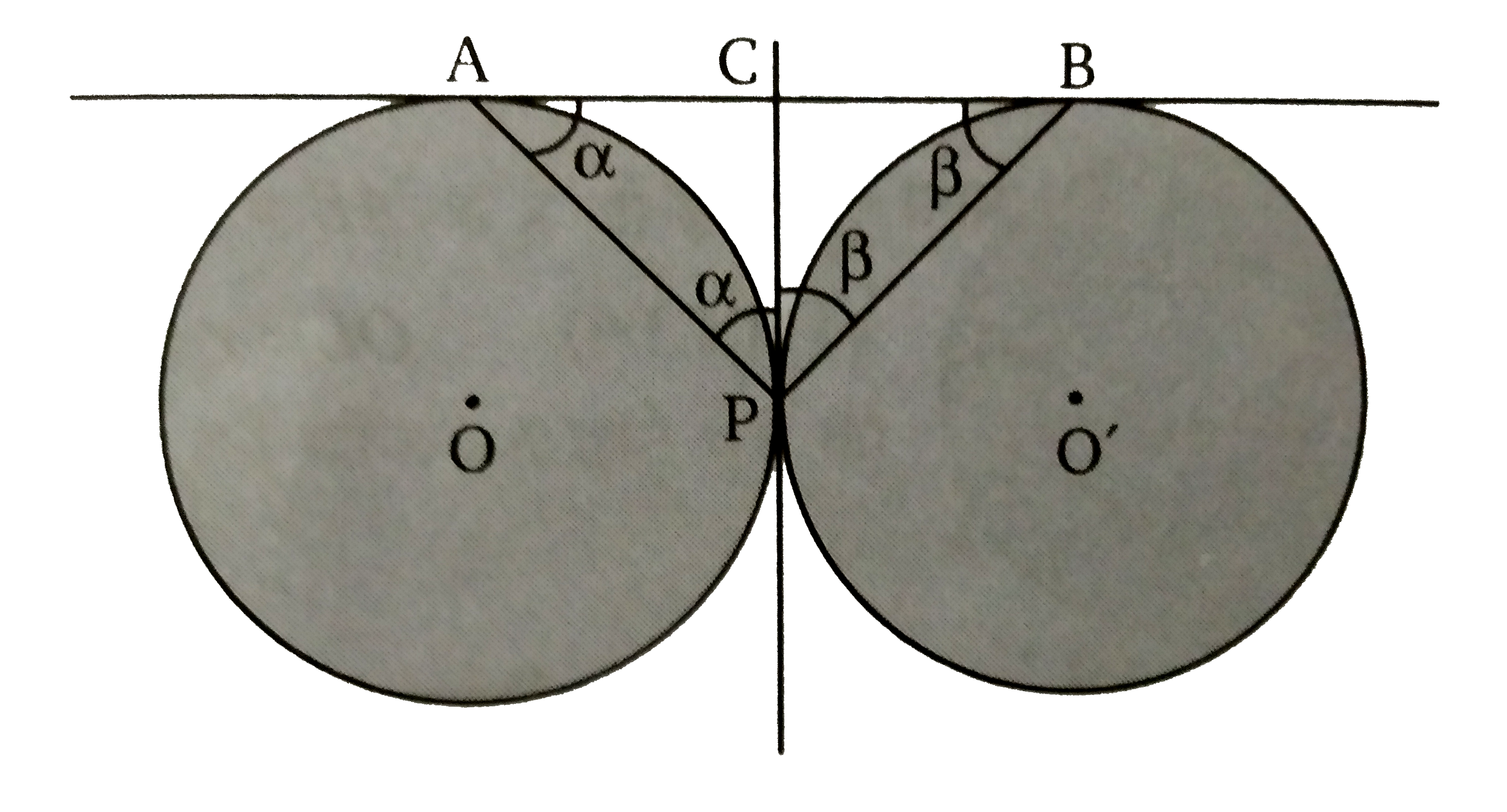
दो वृतों के केंद्रों O व O' है। जो परस्पर बाह्यतः बिन्दु P पर स्पर्श करते हैं। इन वृतों की एक उभयनिष्ठ अनुस्पर्श रेखा AB खींची गई है। सिद्ध कीजिए कि ∠APB=90∘
माना C(O, r) व C(O', r') दो वृत्त हैं।
माना दोनों के स्पर्श बिन्दु पर एक उभयनिष्ठ स्पर्श रेखा PC है तो AB को बिन्दु C पर कटती है। अब क्योंकि CA व CP बाह्य बिन्दु C से केंद्र O वाले वृत्त दो स्पर्श रेखाऐं हैं।
CA = CP
इसलिए ACP एक समद्विबाहु त्रिभुज है। जिसमे
∠PAC=∠APC=α (माना)
इसी प्रकार CB = CP
अतः BCP एक समद्विबाहु त्रिभुज है। जिसमे
∠PBC=∠BPC=β (माना)
अब ΔAPB में, α+(α+β)+β=180∘
⇒2α+2β=180∘⇒α+β=90∘⇒∠APB=90∘
Topper's Solved these Questions
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - अभ्यास प्रश्न 8.1 (अतिलघु उत्तरीय प्रश्न)
4 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - अभ्यास प्रश्न 8.1 (लघु उत्तरीय प्रश्न - II)
2 Videos
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - स्वमूल्यांकन परीक्षण
18 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
6 सेमी त्रिज्या के वृत्त के केन्द्र से 8 सेमी दूर स्थित एक बिंदु से खींची गई स्पर्श रेखा की लम्बाई ज्ञात कीजिये ।
View Solutionएक बिंदु A वृत्त केन्द्र से 26 सेमी दूर है तथा A से वृत्त पर स्पर्शी की लम्बाई 24 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए ।
View Solutionनिम्नलिखित संख्या-युग्मो के HCF ज्ञात कीजिए ।
(i) 156, 13
(ii) 1001, 385
(iii) 81445, 687897
View Solution6 सेमी त्रिज्या वाले वृत्त पर 60∘ पर त्रिज्यखण्ड का क्षेत्रफल व परिमाप ज्ञात कीजिए ।
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionदो वृत्त जिसकी त्रिज्याएँ 3 सेमी एवं 4 सेमी है। जिनके केन्द्रो के बाध्य की दूरी 8 सेमी है। दोनों वृतो पर उभयनिष्ठ स्पर्श रेखाएं कीतिनि खींची जा सकती है ?तथा दो उभयनिष्ठ अनुस्पर्श रेखाओ की रचना कीजि।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त एक दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ की संख्या लिखिये।
View Solutionदो वृत्त जिनकी त्रिज्याएँ 4 सेमी और 3 सेमी है तथा दोनों के केन्द्रो कि मध्य दूरी 6.5 सेमी हैकि रचना कर उन पर एक उभयनिष्ठ अनुस्पर्श रेखा कि रचना कीजिए।
View Solutionदो वृत्त 2.5 सेमी एवं 1 सेमी त्रिजियो के केंद्र परस्पर 7 सेमी दूरी पर है। एक उभयनिष्ठ तिर्यक स्पर्श रेखा कि रचना कीजिए।
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solution
