M1,M2 तथा M3 द्रव्यमान के तीन गुटके एक क्षैतिज मेज पर एक-दूसरे के ऊपर चित्र के अनुसार रखे हैं।
(i) प्रत्येक गुटके का बल निदेशक आरेख बनाइए।
(ii) सम्पर्क तलों की प्रतिक्रिया R1,R2 एवं R3 का मान ज्ञात कीजिए।
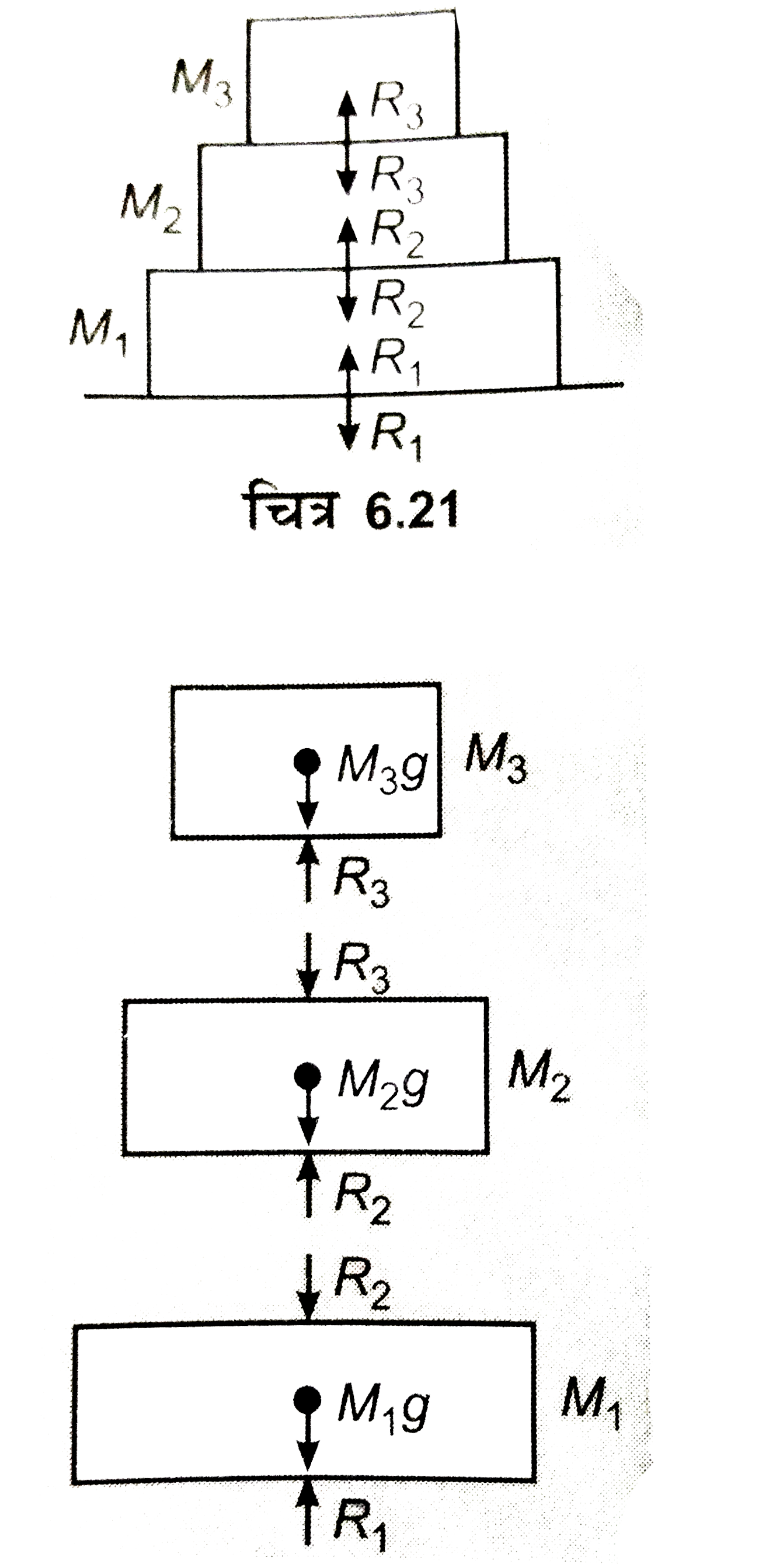
(i)निकाय के विभिन्न भागों पर कार्यरत बल हैं
1. प्रत्येक गुटके पर उसका भार (नीचे की ओर)
2. M1 व क्षैतिज तल के सम्पर्क भाग पर प्रतिक्रिया R1 जोकि तल द्वारा M1 पर ऊपर की ओर तथा M1 द्वारा तल पर नीचे की ओर लगाया जाता है।
3. M1−M2 सम्पर्क तल पर प्रतिक्रिया बल R2 जोकि M1 द्वारा M2 पर ऊपर की ओर तथा M2 द्वारा M1 पर नीचे की ओर लगाया जाता है।
4. M2−M3 सम्पर्क तल पर प्रतिक्रिया बल R3 जोकि M2 द्वारा M3 पर ऊपर की ओर तथा M3 द्वारा M2 पर नीचे की ओर लगाया जाता है।
उपर्युक्त बलों के आधार पर गुटके M1,M2 एवं M3 के बल निदेशक आरेख चित्र में प्रदर्शित हैं

M3 के संतुलन के लिए
R3−M3g=0
∴R3=M3g
M2 के संतुलन के लिए
R2−R3−M2g=0
∴R2=R3+M2g=M3g+M2g
=(M2+M3)g
M1 के संतुलन के लिए
R1−R2−M1g=0
∴R1=R2+M1g=(M2+M3)g+Mg
=(M1+M2+M3)g
Topper's Solved these Questions
- न्यूटन के गति के नियमBOOK - BALAJI PUBLICATIONCHAPTER - न्यूटन के गति के नियमEXERCISE - प्रश्नावली (लघु उत्तरीय प्रश्न)
16 Videos
- न्यूटन के गति के नियमBOOK - BALAJI PUBLICATIONCHAPTER - न्यूटन के गति के नियमEXERCISE - प्रश्नावली (दीर्घ उत्तरीय प्रश्न)
6 Videos
- द्रव्यमान केन्द्र BOOK - BALAJI PUBLICATIONCHAPTER - द्रव्यमान केन्द्र EXERCISE - अभ्यास के लिए प्रश्न
2 Videos
- पृष्ठ तनावBOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठ तनावEXERCISE - बहुविकल्पीय प्रश्न
38 Videos
Similar Questions
बल का SI मात्रक तथा विमीय सूत्र लिखिए।
View Solutionन्यूटन की गति का प्रथम नियम लिखिए। इस नियम के दो उदाहरण दीजिए।
View Solution2 किग्रा तथा 1 किग्रा द्रव्यमान के दो पिण्ड 3 मीटर की दूरी पर स्थित है | निकाय के द्रव्यमान केन्द्र की स्थिति ज्ञात कीजिये |
View Solutionद्रव का पृष्ठ तनाव -
View SolutionTwo planets of radii R_(1) and R_(2 have masses m_(1) and M_(2) such that (M_(1))/(M_(2))=(1)/(g) . The weight of an object on these planets is w_(1) and w_(2) such that (w_(1))/(w_(2))=(4)/(9) . The ratio R_(1)/R_(2)
View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are
View Solutionद्रव्यमान केंद्र क्या है ? द्विकण निकाय के लिए सिद्ध कीजिए कि −−→rcm=m1→r1+m2→r2m1+m2
जहाँ संकेतों के सामान्य अर्थ हैं ।
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View SolutionPosition vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View Solution1 किग्रा, (32) किग्रा, एवं 2 किग्रा द्रव्यमानों के तीन कण a भुजा वाले एक समबाहु त्रिभुज के शीर्षों पर रखे गये हैं। द्रव्यमान केन्द्र के X, Y निर्देशांक होंगे-
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are
View SolutionTwo planets of radii R1 and R2 have masses m1 and M2 such that M1M2=1g. The weight of an object on these planets is w1 and w2 such that w1w2=49. The ratio R1R2
View SolutionTwo satellites of masses m1 and m2(m1>m2) are revolving the earth in circular orbits of radius r1 and r2(r1>r2) respectively. Which of the following statement is true regarding their velocities v1 and v2.
View Solutionमान लीजिये r1 और r2 पर स्थित दो द्रव्यमानो m1 तथा m2 के बीच गुरुत्वाकर्षण बलों F1 तथा F2 के लिए न्यूटन के गुरुत्वाकर्षण नियम को F1=−F2=−r12r312GM20(m1m2M20)n द्वारा व्यक्त किया जाता है। यहाँ M0 एक स्थिरांक है जिसकी विमा द्रव्यमान की है। r12=r1−r2 तथा n कोई संख्या है। ऐसे प्रकरण में
View Solution
