On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).

The correct Answer is:B, C, D
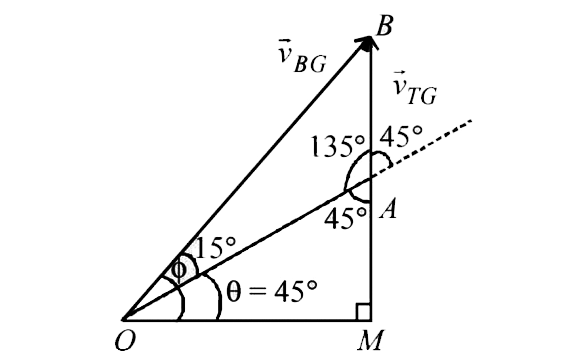
(a) Let the ball strike the trolley at B . Let
→vBG= velocity of ball w.r.t. ground
→v(TG)=velocityoftrol≤ye.r.tground
∴ Velocity of ball w.r.t. trolley
→v(BT)=→v(BG)−→v(TG)…..(i)
From triangles OAB
−−→OA+−−→AB=−−→OB
∴−−→OA+→vTG = vec v(BG)<br> :. vec(OA) = vecv_(BG) - vecv_(TG)....(ii)<br>From(i)and(ii)vec(OA) = vecv _(BT)<br>rArrvelocityofballw.r.t.trol≤ymakesan∠of 45(@)withthe X-axis <br>(b)Here theta = 45(@) <br>:. phi = (4 theta)/(3) = (4 xx 45)/(3) = 60(@)<br>InDeltaOMA, ltbr gt θ=45(∘)⇒∠OAM=45(∘)
∴∠OAB=135(∘)
Also ∠BOA=60(∘)−45(∘)=15(∘)
Using since law in ΔOBA
vBGsin135(∘)=vTGsin15(∘)⇒vBG=2m/s

Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with timeBincreases with timeCremains constantDis zeroA straight line makes an angle of 135∘ with the X-axis and cuts Y-axis at a distance -5 from the origin. The equation of the line is
A2x+y+5=0Bx+2y+3=0Cx+y+5=0Dx+y+3=0A straight line which makes an angle of 60∘ with each of Y and Z-axis, the angle this lines makes with X-axis is
A30∘B60∘C75∘D45∘
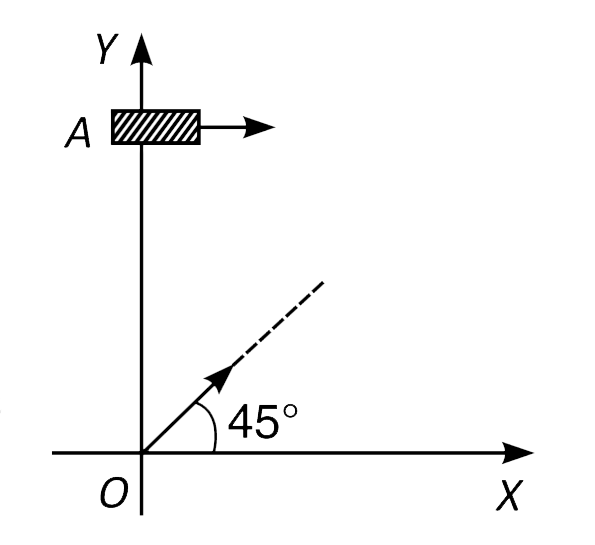
A small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4m/s2. Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart.
(a) Describe the path of the ball in a reference frame attached to the cart.
(b) Find the speed of the ball.
View SolutionEquations of Lines Parallel to the X-axis and Y-axis
View SolutionThe equation of a straight line which makes an angle 45∘ with the x-axis with y-intercept 101 units is :
View SolutionThe equation of a straight line which makes an angle 45° with the x-axis with y-intercept 101 units is
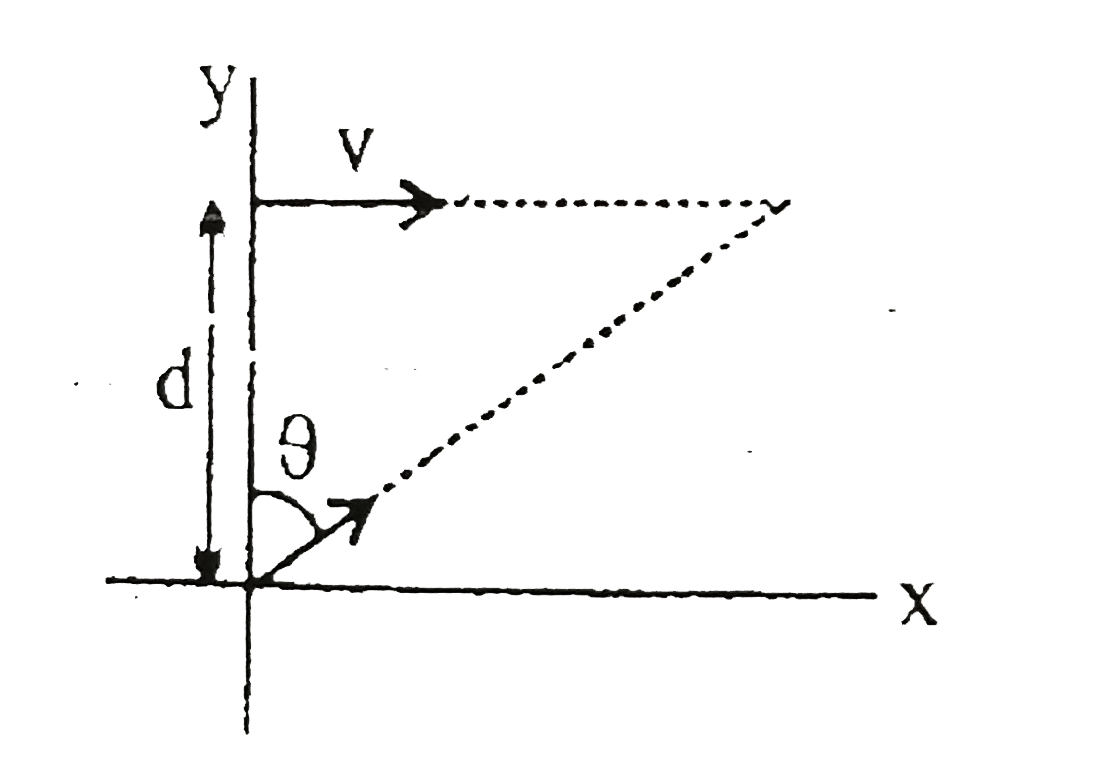
View SolutionA particle moves along a straight line parallel to x-axis at a distancce d=3m from it, with constant speed of v=3m/s. Another particle stats from the origin with constant acceleration a=4m/s2 at an angle θ with y-axis along a straight line at the instant the first particle crosses y-axis. Find 'theta' such that the two particle collide.
View Solution

