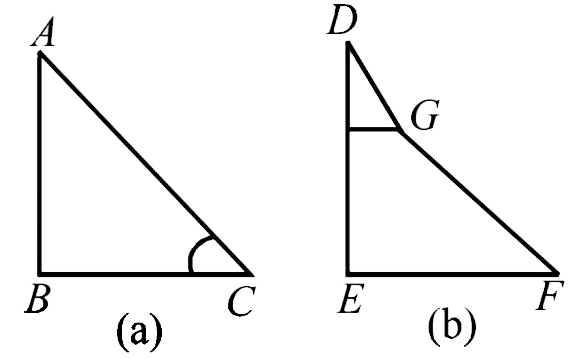
In the figure (a) and (b) and are fixed inclined planes and A small block of mass is rdeased from the point it sides down and maches with a speed The same block is relessed from rest from the point it sides down and reached the point the with ACDGFmuV_(C) (p)
The correct Answer is:B, C
(a) K.E at (1)/(2) mv_(F)^(2)= mgy - mu mg cos a DG - mumg cos beta GF(1)/(2)v_(F)^(2) = gy - mu (GM)/(DG) xx DG - mug (FN)/(GF)xx GF :. (1)/(2) v_(F)^(2) = gy - mug (GM + FN):. V_(p) = sqrt(2g (y -mu x) (##JMA_WEP_C04_026_S02.png" width="80%">
Topper's Solved these Questions
Similar Questions
Block of mass m are released from rest and they slide down the inclined surface as shown in figure. Show that the work done by the frictional forces on the blocks are same in all the cases. Also calculate the speeds with which the blocks reach point B. The coefficient of friction for all the surface is μk.

View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View Solution
Knowledge Check
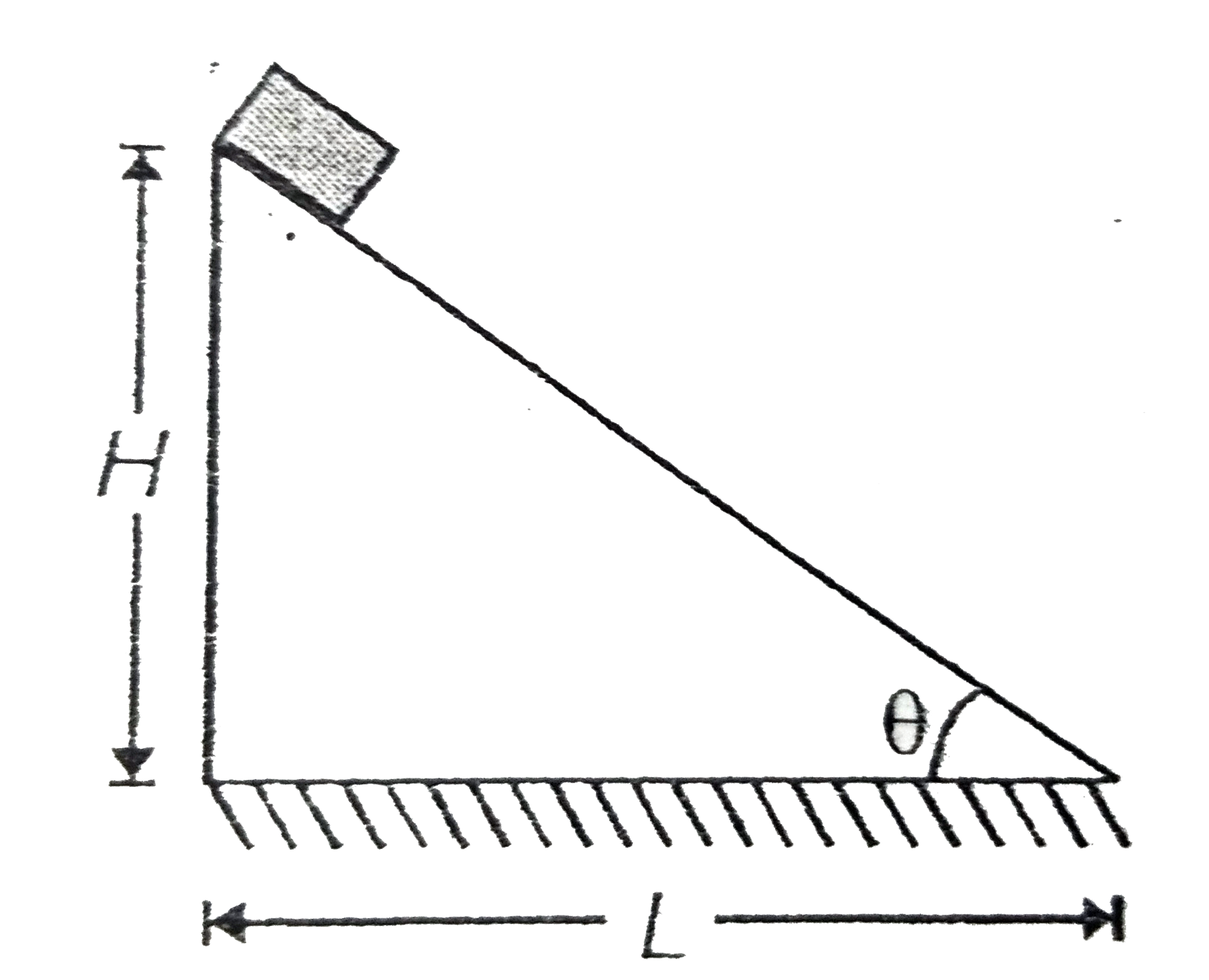
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)A block of mass m released from rest from point O as shown below. The velocity of the block at the lowest points are v O , v E, v F respectively. Assume coefficient of kinetic friction between surface and the block is same in all cases. Then,
(a)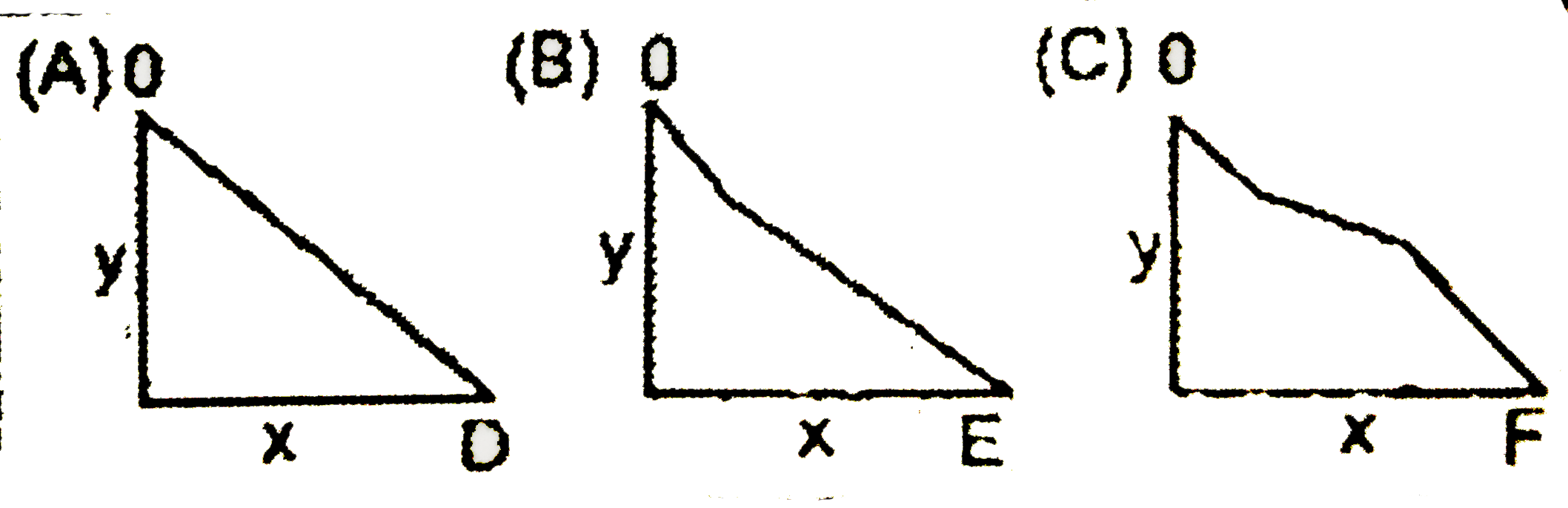 AvD>vE>vFBvf>vE>vDCvD=vE=vFDvD=vEvF=0
AvD>vE>vFBvf>vE>vDCvD=vE=vFDvD=vEvF=0A block of mass M slides down a rough inclined surface of inclination θ and reaches the bottom at speed at 'v' . However , if it slides down a smooth inclined surface of same length and same inclination , it reaches the bottom with the speed kv. Coefficient of friction between the block and the rough incline is :
Asinθ(k2−1)B(k2−1k2)tanθC(k2+1k2)cosθDk2−1k2
A block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionA body freely released from A slides down a smooth inclined plane 'AB' and then a rough incline plane 'BC' such that BC = N (AB). If the block comes to rest at C, then coefficient of kinetic friction between the block and inclined plane is?
View Solution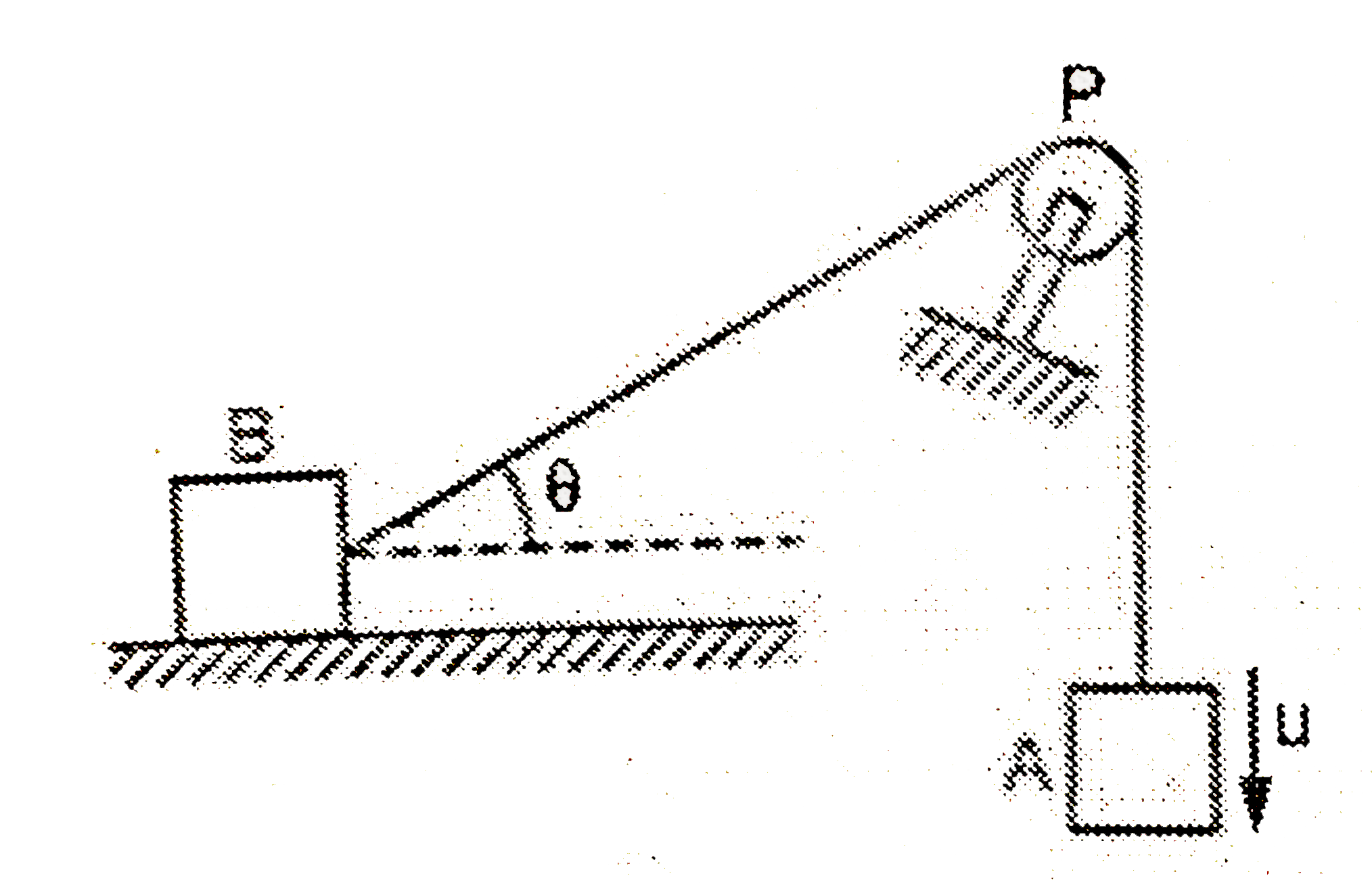
In the figure, the blocks are of equal mass. The pulley is fixed. In the position shown, A moves down with a speed u, and vB= the speed of B.
View SolutionA block released from rest from the top of a smooth inclined plane of inclination 45∘takes time 't' to reach the bottom . The same block released from rest , from top of a rough inclined plane of same inclination , takes time '2t' to reach the bottom , coefficient of friction is :
View Solution
