A bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
 .
.
θ=π4
π4<θ<π2
π2<θ<3π4
3π4<θ<π
The correct Answer is:D
(d) This is the case of vertical motion when the body just
completes the circle. Here
v=√5gL…..(i)
Applying energy conservation,
Total energy at A = Total energy at P
12mv2=)1)2m(v2)2+mgh.<br>rArr h = (3v^2)/(8g)<br>= (3)/(8g)xx5gL = (15L)/(8)....(ii)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_RM_C06_032_S01.pngwh=80%mx-autosty≤=background:white;><br>InDelta OPM, cos theta = (L -h)/(L) = ((L - (15L)/(8)/(L) = (-7)/(8)<br>Therefore,thevalueofthetalies∈theran≥(3pi)/(4) ltthetaltpi.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
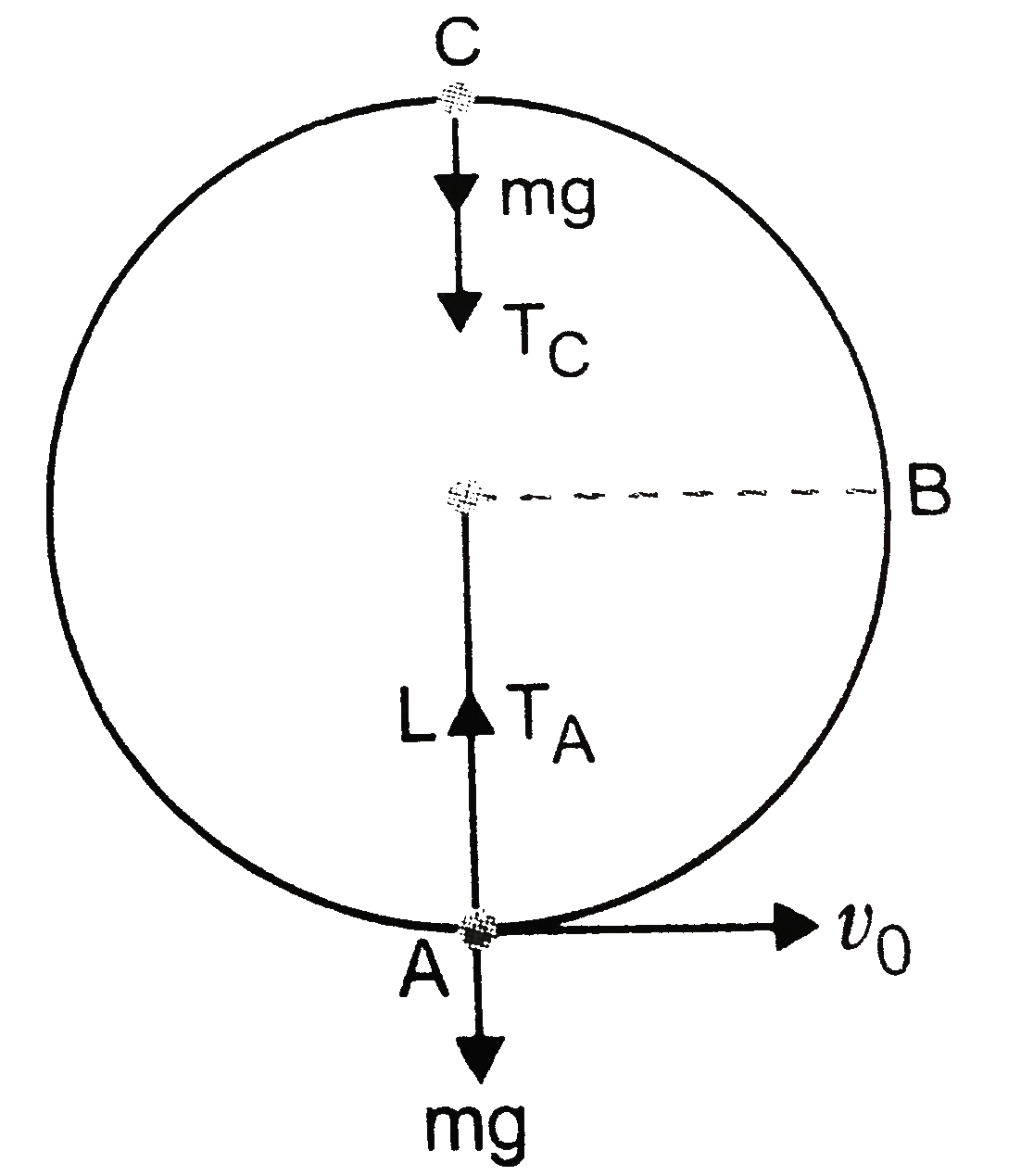
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
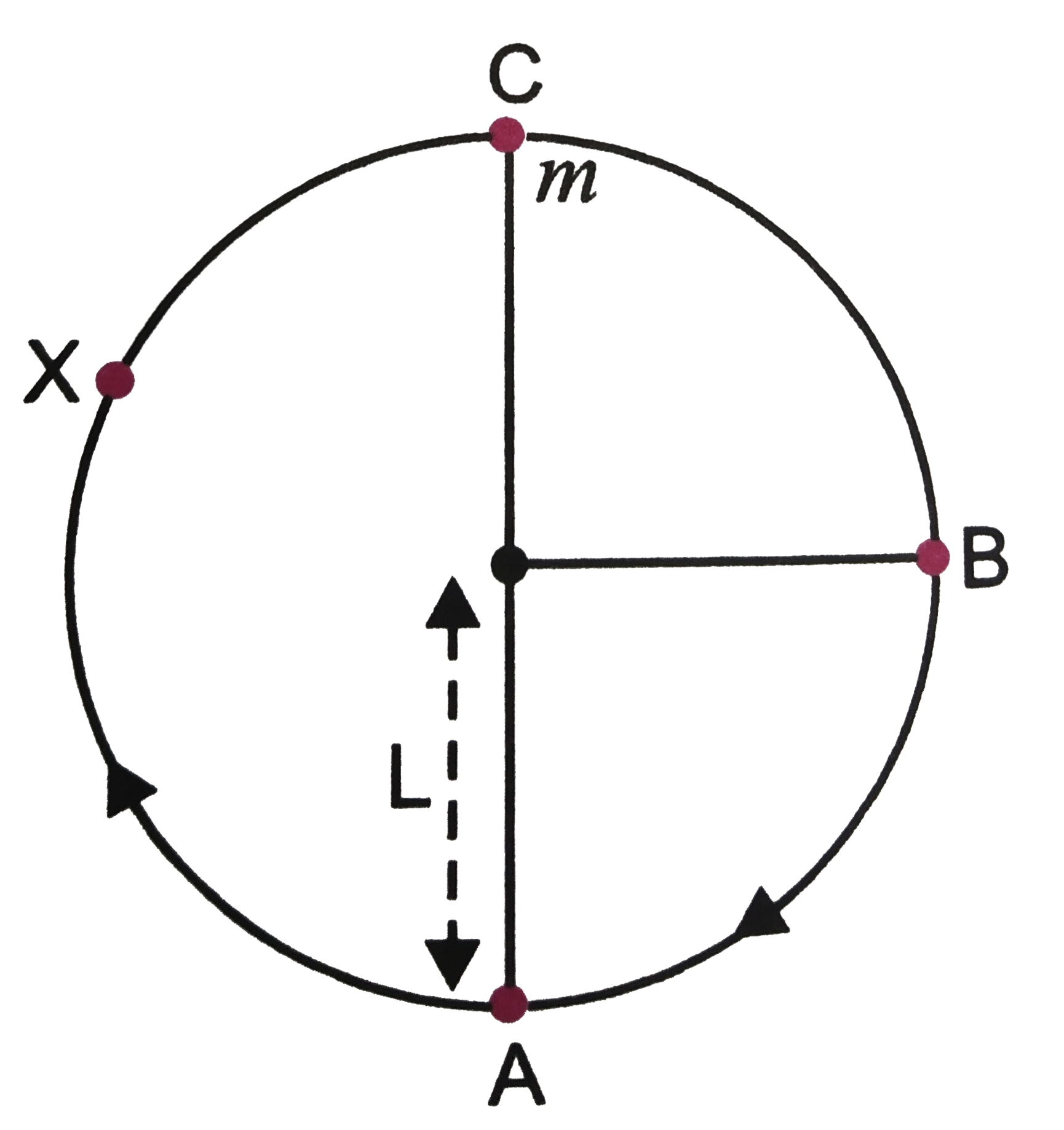
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
View Solution
Knowledge Check
A mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6glThe bob of a simple prendulum is suspended by a strinng of length 80 cm . What minimum horizontal velocity should be imparted to the bob so that it reaches it reaches the height of suspension point ? (g=10m/s2)
A3m/sB4m/sC2m/sD5m/sA simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–
 Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2
Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2
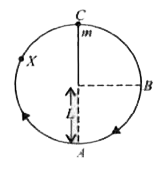
A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
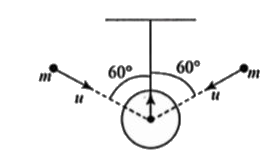
View SolutionA bob of mass 10 M is suspended through an inextensible string of length I. When the bob is at rest at the equilibrium position, two particles of mass m each moving with velocity u making an angle 60° with the string strike and get simultaneously attached to the bob. What is the value of impulsive tension (Jtension) be string during the impact?
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet is
View Solution
