The figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separated. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,
the point O has linear velocity 3Rωˆi
the point P has linear velocity 114Rωˆi+√34Rωˆk.
the point P has linear velocity 134Rωˆi−√34Rωˆk
the point P has linear velocity ((3−√34)Rωˆi+14Rωˆk.
The correct Answer is:A, B
(a,b) For rolling motion, the velocity of the point of contact
with respect to the surface should be zero. For this
3Rω(−ˆi)∣→v0=0∴→v0=3Rωˆi
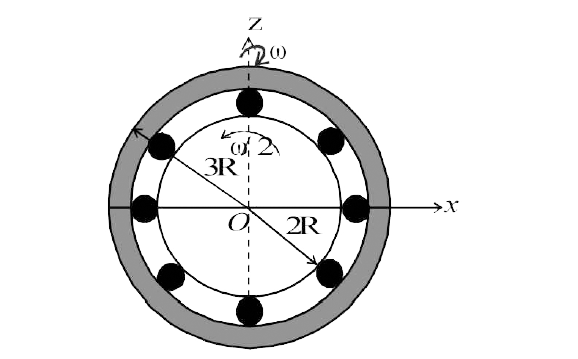
A shown in the figure, the point P will have two
velocities
(i) 3Rωˆi (due to translational motion)
(ii) R2ω making an angle fo 30∘ with the vertical due
to rotation
∴→up=[3Rωˆi−Roemga4ˆi]+√3Rω4ˆk
=114Rωˆi+√34Rωˆk.
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer1videos
ROTATIONAL MOTION
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced63videos
MOTION
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced69videos
SIMPLE HARMONIC MOTION
Similar Questions
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
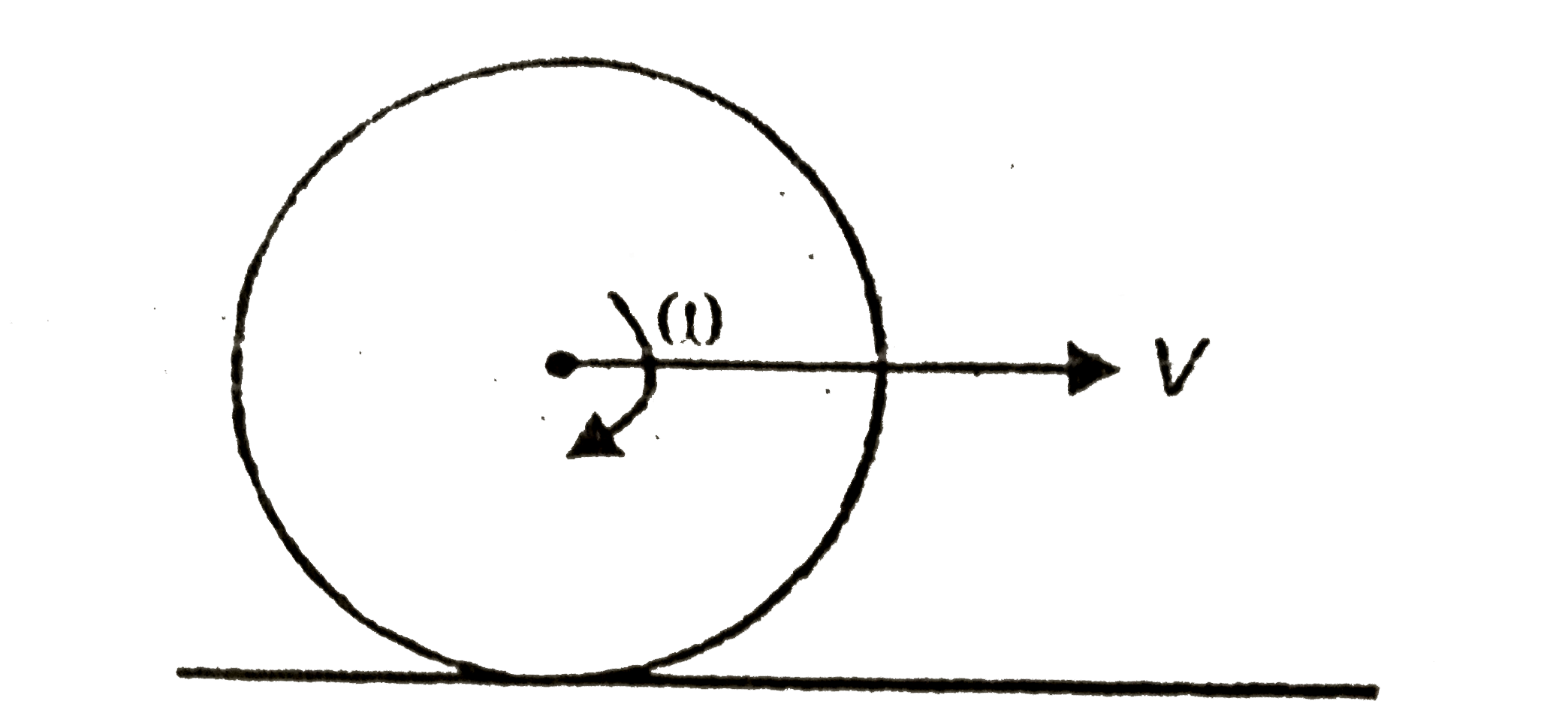
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ring and a disc of same mass roll without slipping along a horizontal surface with same velocity. If the K.E. of ring is 8J, then that of disc is
A2JB4JC6JD16J - Question 2 - Select One
A thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
 Apω2r2/2Bpω2r2Cpω2r2/3DNone
Apω2r2/2Bpω2r2Cpω2r2/3DNone - Question 3 - Select One or More
A rough disc of mass m rotates freely with an angular velocity ω. If another rough disc of mass m2 and same radius but spinning in opposite sense with angular speed ω is kept on the first disc. Then:
Athe final angular speed of the dise is ω3Bthe net work does by friction is zeroCthe friction does a positive work on the lighter discDthe net work done by friction is −mR2ω23
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
 View Solution
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.View Solution

