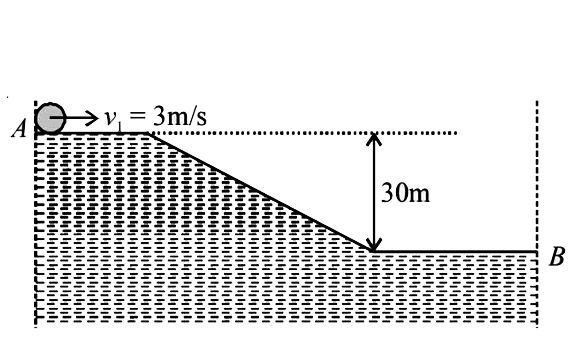
Two identical uniform discs roll without slipping on tow different sufaces AB and CD (see figure) starting at A and C with linear speeds respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed

Total kinetic energy of a rolling disc
For surface AB
For surface CD(3)/(4)m (v_2)^2 +mg(27) = (3)/(4)mV_D^2 ....(ii)V_B =B_D.(3)/(4)m(3)^2+mgxx30 =(3)/(4)m(v_2)^2 + mgxx27:.v_2 =7
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Knowledge Check
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)Two identical photo-cathodes receive light of frequencies v1 and v2. If the velocities of the photoelectrons (of mass m) coming out are v1 and v2 respectively, then
Av1−v2=[(2hm)(v1−v2))]1/2Bv21−v22=2hm(v1−v2)Cv1−v2=[(2hm)(v1−v2))]1/2Dv21−v22=2hm(v1−v2)Two identical cylinders roll from rest on two identical planes of slant lengths s and 2s but of the same height h. Then, the velocities, v1 and v2 acquired by the cylinders when they reach the bottom of the incline are related as.
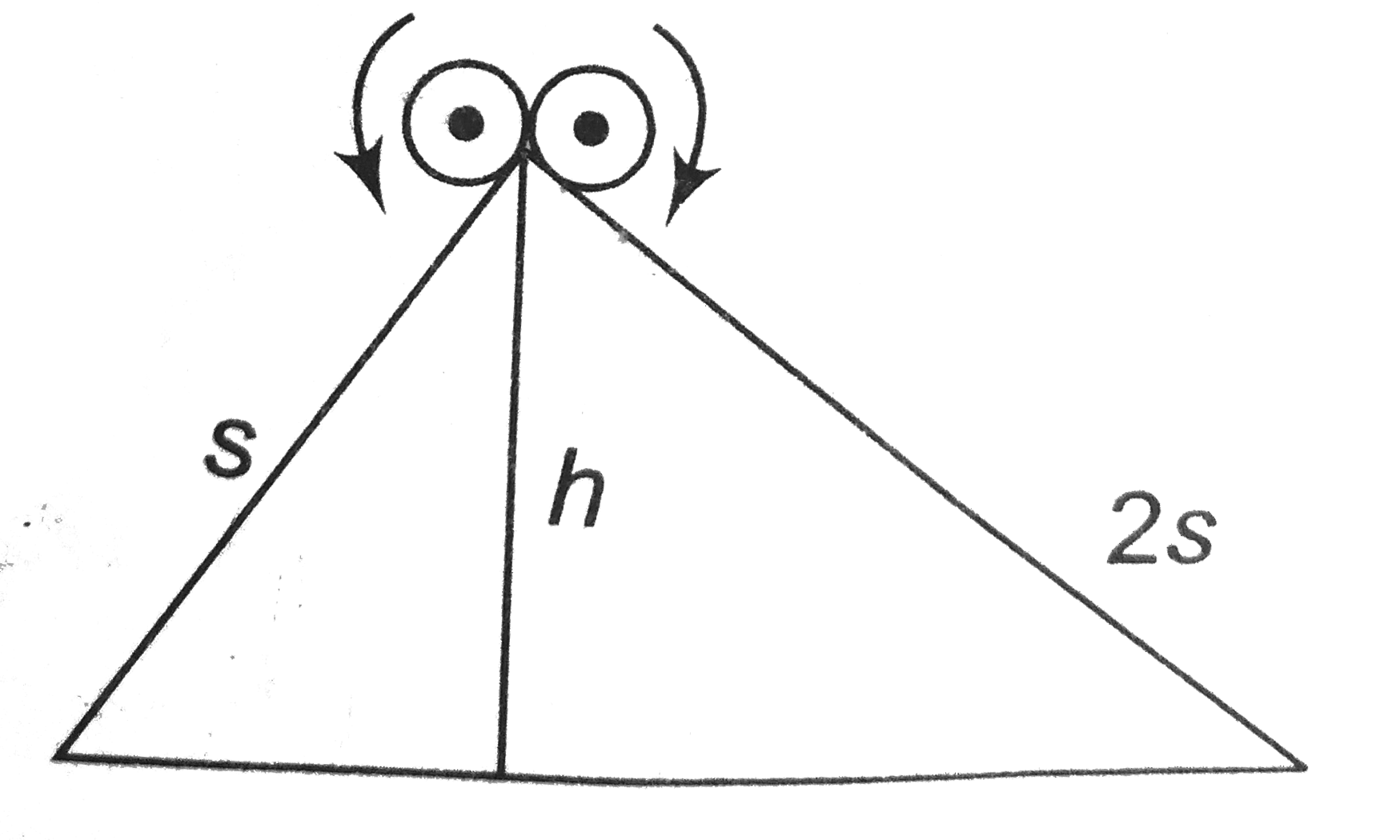 .Av1=v2Bv1=2v2C2v1=v2DNone of the above.
.Av1=v2Bv1=2v2C2v1=v2DNone of the above.

Particle P shown in figure is moving in a circle of radius R=10 cm with linear speed v=2m/s Find the angular speed of particle about point O.
View SolutionWhat will be the reading of spring balance in the figure shown in following situations ( g=10m/s2 )
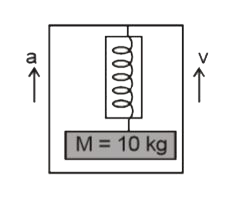
a=2m/s2,v=0
View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
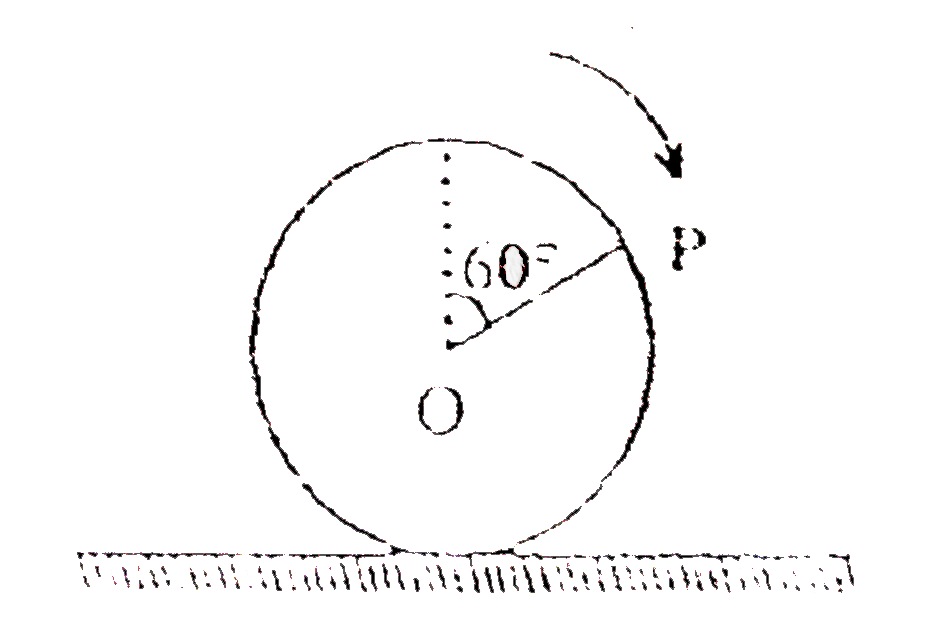
View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find the linear speed at point C.
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View Solution

