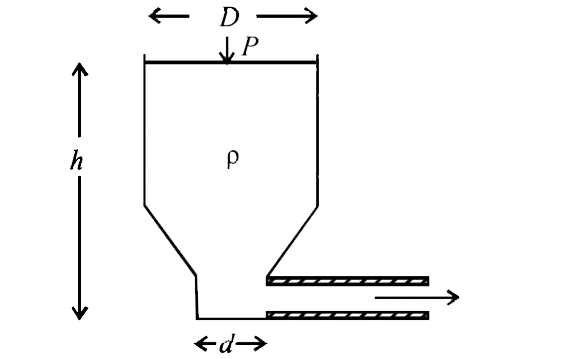
Shown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of $v_{0}$ . The density of the liquid is given as $ρ$ . Calculate the coefficient of viscosity $η$ .

Text Solution

Verified by Experts

The correct Answer is:A, B, D

Updated on:21/07/2023

The rate of flow of a liquid through a capillary tube is
Adirectly proportional to the length of tube.
Binversely proportional to the difference of pressure between the ends of the tube.
Cdirectly proportional to the $4^{t h}$ power of the radius of the tube.
Dindependent of the nature of the liquid.
A liquid of density $900 \frac{k g}{m^{3}}$ is filled in a cylindrical tank of upper radius 0.9 m and lower radius 0.3 m A capillary tube of length 1 is attached at the bottom of the tank as shown in fig. The capillary has outer radius 0.002 m and inner radius a. When pressure P is applied at the top of the tank volume flow rate of liquid is $8 \times 10^{- 6} \frac{m^{3}}{s}$ and if capillary tube is detached, the liquid comes out from the tank with a velocity $10 \frac{m}{s}$ . then the coefficient viscosity of liquid is $\frac{π a^{2} = 10^{- 6} m^{2} a^{2}}{l = 2 \times 10^{- 6} m}$ .
A $η = 1.25 \times 10^{- 3} N - \frac{s}{m^{2}}$
B $η = 2.50 \times 10^{- 3} N - \frac{s}{m^{2}}$
C $η = 5.00 \times 10^{- 3} N - \frac{s}{m^{2}}$
D $η = 7.25 \times 10^{- 3} N - \frac{s}{m^{2}}$
When two capillary tubes of different diameters are dipped vertically in a liquid , the rise of the liquid in the capillary tube
Ais same in both tubes
Bis more in tube of larger diameter
Cis more in tube of smaller diameter
Dthere is no rise of liquid in capillary tube of larger diameter.