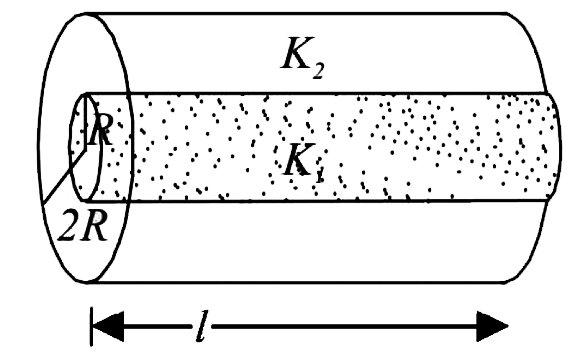
A cylinder of radius R made of a material of thermal conductivity is surrounded by a cylinderical shell of inner radius R and outer radius 2R made of a material of thermal conductivity . The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effictive thermal conductivity of the system is
The correct Answer is:C
(c) Total transfer of heat per second through the composite
=Heat transfer per second from material with thermal
conductivity +Heat transfer per second from
material with thermal conductivity
or, Kpi(2R)^2=K_1piR^2+K_2pi[(2R)^2-R^2]K=(K_1+3K_2)/4
Topper's Solved these Questions
Similar Questions
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionA cylinder of radius R, made up of a material (thermal conductivity k1) is surrounded by a cylindrical sheet of inner radius R and outer radius 2R (thermal conductivity k2). The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Calculate the effective thermal conductivity of the system.
View Solution
Knowledge Check
A cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
AK1+K2BK1+8K29CK1K2K1+K2D8K1+K29A cylinder A of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperature. if the effective thermal conductivity of the system is 4K1+5K29, find the rate of outer radius of the shell to the radius of the cylinder.
 A2.0B5/2C5/3D3/2
A2.0B5/2C5/3D3/2The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
Aheat flows in the rod from high temperature to low temperature even if the rod has nonuniform cross sectional area.Btemperature gradient along length is same even if the rod has non uniform cross sectional area.Cheat current is same even if the rod has nono-uniform cross sectional areaDif the rod has uniform cross sectional area the temperature is same at all points of the rod.
A cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionCalculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r1and r2. Assume that thermal conductivity of the material is K
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
View SolutionA metallic cylindrical shell of length 50 cm has inner radius of 3 cm and outer radius of 6 cm. If the inner and outer surfaces of the cylinder are maintained at 0∘C and 80∘C , respectively, then find the rate of flow of heat from the outer surface to the inner surface. Take, thermal conductivity of metal =69.3Wm−1k−1
View SolutionA cylinder of radius R and length l is made uo of a substnace whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2 Detemine the effective thermal conductivity between the flat faces of the cylinder
 .
.
View Solution
