A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
The correct Answer is:C, D
Let A be the area of cross-section of the tube.
Since temperature is the same, applying Boyle's law on the
side AB
P×(×xA)=P2×(X2×A)….(i)
Applying Boyle's law in section CD
P×(×xA)=P1×(x1×A)…..(ii)
From (i) and (ii)
P1×(x1×A)=P2×(X2×A)
⇒P1x1=P2x2
where P2=P1+Pressuredue→mercurycolumn

Pressure due to mercury column
P=FA=mgsin30∘A=Vdgsin30∘A
=(A×5)×dgsin30∘A=5sin30∘cmofHg
P2=P1+5sin30∘=P1+2.5
Substituting this value in (iii)
P1×x1=[P1+2.5]×x2
P1×46=[P1+2.5]×44.5
∴P1=44.5×2.51.5
Substituting this value in (ii)
P×x=44.5×2.51.5×46
⇒P×[46+44.52]=44.5×2.51.5×46
[∵x=x1+x22)⇒P=75.4cm
Topper's Solved these Questions
Similar Questions
A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. when the tube is held at and angle of 60∘ with the vertical, the length of the air column above and belw the mercury pellet are 46cm and 44.5cm respectively. Calculate the ressure - in centimeters of mercury, The timperature of the system is kept at 30∘C.
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View Solution
Knowledge Check
A mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
A37.5 cmB75cmC112.5cmD150cmAglass tube scaled at both end is 1m long. It lies horizontally with middle 10cm containing Hg. The two ends of the tube, eqaul in length, contain air at 27∘C Neglect the chang in length of Hg column. Then the change in length on two sides is
A12.3 cmB10.311 cmC9.9cmD8.49cm
A thin tube of uniform cross section is sealed at both ends. It lies horizontally. The middle 5 cm containing Hg and the two equal parts containing air at the pressure P0.When the tube is held at an angle 60∘ with the vertical, the length of air column above and below the mercury are 46 and 44.5 cm respectively. Calculate the pressure P0 in cm of Hg (the temperature of the system is kept at 30∘C).
View SolutionA thin tube, sealed at both ends, is 100cm long. If lies horizontally, the middle 10cm containing mercury and the two equal containing air at stan-dard atmospheric pressure. If the tube is now turned to a verical position, by what amount will the mercury be displaced ?
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View Solution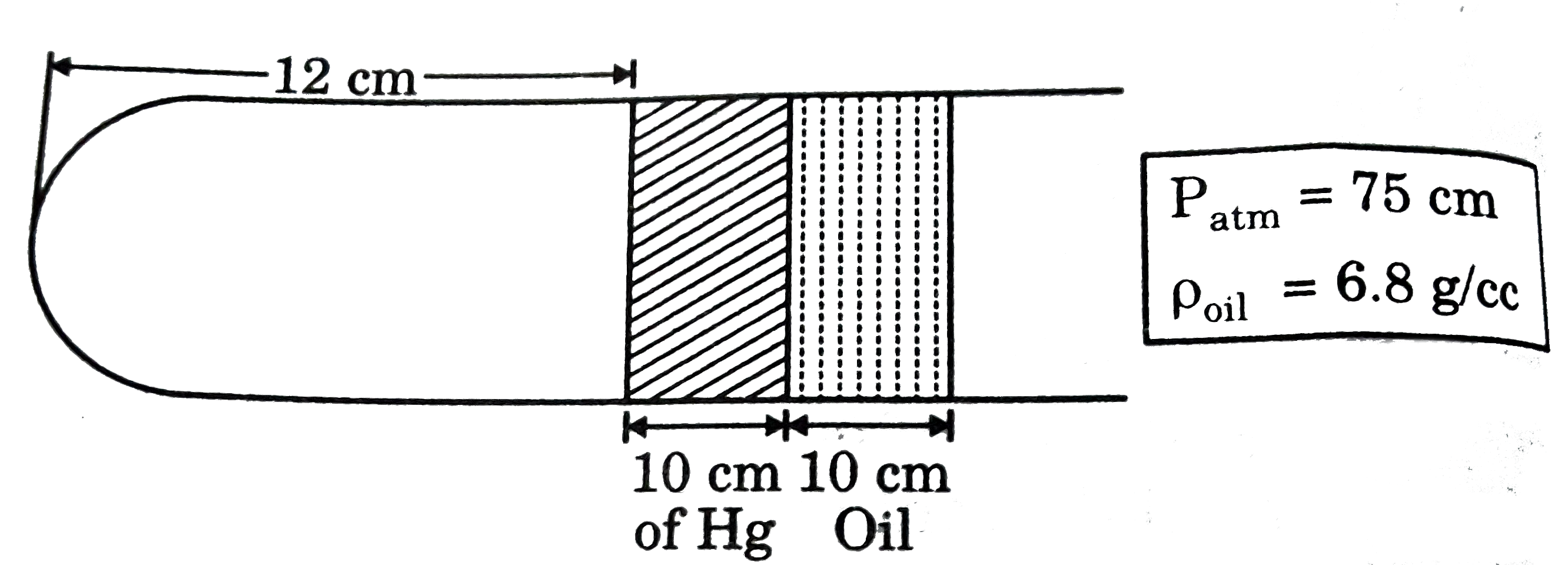
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionIn the given figure a glass tube lies horizontally with the middle 20cm containing mercury. The two ends of the tube contains air at 27∘C and at a pressure 76cm of mercuy. Now the air column on one side in maintained at 0∘C and the other side is maintained at 127∘C. Find the new length of the air column on the cooler side. Neglect the changes in the volume of mercury and of the glass.

View Solution
