Two spherical bodies, A(radius 6cm) and B(radius 18cm) are at temperature T1andT2, respectively. The maximum intensity in the emission spectrum of A is at 500nm and in that of B is at 1500nm. Considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B?
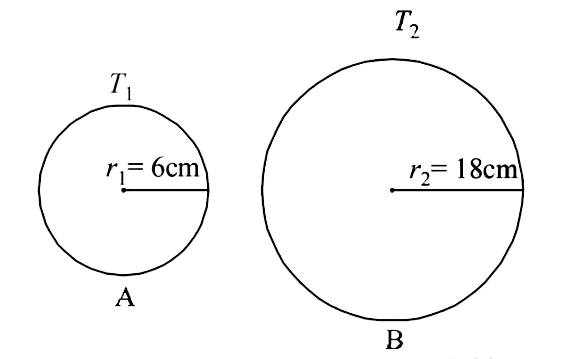
Rateof→tale≠rgyradiatedbyARate→tale≠rgyradiatedbyB
σT41(4πr21)σT42(4πr22)=(T1T2)4×(r1r2)2
=⎛⎝⎛⎝λm2(λm1)4(r1r2)2[∵T1T2=(λm2λm1byWe∈'slaw
=(1500500)4(618)2=9
Topper's Solved these Questions
Similar Questions
Two spherical bodies A (radius 6cm) and B (radius 18cm) are at temperature T1 and T2 respectively The maximum intensity in the emission spectrum of A is at 500nm and in that of B is at 1500nm considering them to be black bodies, what will be the ratio of total energy radiated by A to that of B .
View SolutionA spherical body of area A, and emissivity e = 0.6 is kept inside a black body. What is the rate at which energy is radiated per second at temperature T
View Solution
Knowledge Check
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
A(T1T2)2B(T2T1)2C(T1T2)4D(T2T1)4If the radius of a star is R and it acts as a black body, what would b the temperature of the star, in which the rate of energy production is Q?
A(Q4πR2σ)1/4BQ4πR2σC(Q4πR2σ)D(4πR2Q/σ)1/4Two black bodies A and B have equal surface areas and are maintained at temperatures 27∘C and 177∘C respectively. What will be the ratio of the thermal energy radiated per second by A to that by B?
A4:9B2:3C16:81D27:177
Two bodies A and B at temperatures T1KandT2K respectively have the same dimensions. Their emissivities are in the ratio of 1:3. If they radiate the same amount of heat per unit area per unit time, then the relation between their temperatures is given by
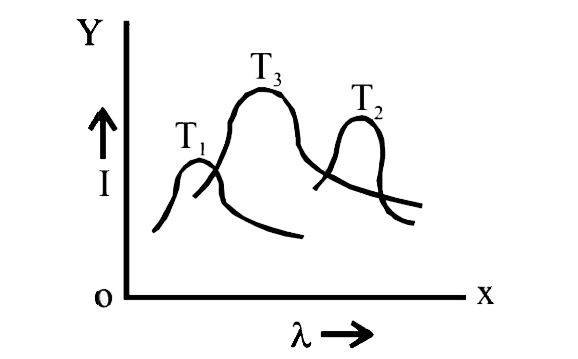
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
View SolutionTwo stars A and B radiate maximum energy 5200Å and 6500Å respectively. Then the ratio of absolute temperatures of A and B is
View SolutionA black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
View SolutionA black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
View Solution
