Three perfect gases at absolute temperature T1,T2,andT3 are mixed. The masses of molecules are n1,n2andn3 respectively. Assuming to loss of energy, the final temperature of the mixture is:
n1T1+n2T2+n3T3n1+n2+n3
n1T21+n2T22+n3T23n1T1+n2T2+n3T3
n21T21+n22T22+n23T23n1T1+n2T2+n3T3
(T_1+T_2+T_3)/3
The correct Answer is:A
To find the final temperature of the mixture of three perfect gases at absolute temperatures T1,T2, and T3 with respective masses of molecules n1,n2, and n3, we can follow these steps:
Step 1: Understand the Concept of Kinetic Energy
The total kinetic energy of a gas is related to its temperature and can be expressed as:
E=32PV
where P is the pressure and V is the volume of the gas.
Step 2: Calculate the Initial Energies
For each gas, the initial energy can be expressed as:
- For gas 1:
E1=32P1V1
- For gas 2:
E2=32P2V2
- For gas 3:
E3=32P3V3
Step 3: Relate Energy to Moles
Using the ideal gas law PV=nRT, we can express the energies in terms of the number of moles n:
- The number of moles for each gas is given by:
n1=N1NA,n2=N2NA,n3=N3NA
where NA is Avogadro's number.
Step 4: Write the Total Energy Equation
Assuming no energy loss during mixing, the total initial energy is equal to the final energy:
E1+E2+E3=Efinal
This can be written as:
32P1V1+32P2V2+32P3V3=32PfinalVfinal
Step 5: Substitute the Ideal Gas Law
Substituting PV in terms of moles and temperature:
32(N1NART1+N2NART2+N3NART3)=32(N1+N2+N3NARTmix)
Step 6: Cancel Common Terms
Cancel 32 and NA from both sides:
N1T1+N2T2+N3T3=(N1+N2+N3)Tmix
Step 7: Solve for Final Temperature
Rearranging gives us:
Tmix=N1T1+N2T2+N3T3N1+N2+N3
Final Result
Thus, the final temperature of the mixture is:
Tmix=n1T1+n2T2+n3T3n1+n2+n3
The total kinetic energy of a gas is related to its temperature and can be expressed as:
E=32PV
where P is the pressure and V is the volume of the gas.
For each gas, the initial energy can be expressed as:
- For gas 1:
E1=32P1V1
- For gas 2:
E2=32P2V2
- For gas 3:
E3=32P3V3
Using the ideal gas law PV=nRT, we can express the energies in terms of the number of moles n:
- The number of moles for each gas is given by:
n1=N1NA,n2=N2NA,n3=N3NA
where NA is Avogadro's number.
Assuming no energy loss during mixing, the total initial energy is equal to the final energy:
E1+E2+E3=Efinal
This can be written as:
32P1V1+32P2V2+32P3V3=32PfinalVfinal
Substituting PV in terms of moles and temperature:
32(N1NART1+N2NART2+N3NART3)=32(N1+N2+N3NARTmix)
Cancel 32 and NA from both sides:
N1T1+N2T2+N3T3=(N1+N2+N3)Tmix
Rearranging gives us:
Tmix=N1T1+N2T2+N3T3N1+N2+N3
Thus, the final temperature of the mixture is:
Tmix=n1T1+n2T2+n3T3n1+n2+n3
Topper's Solved these Questions
Similar Questions
Two perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View SolutionTwo perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View Solution
Knowledge Check
Three perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
A(T1+T2+T3)3Bn1T1+n2T2+n3T3n1+n2+n3Cn1T21+n2T22+n3T23n1T1+n2T2+n3T3Dn21T21+n22T22+n23T23n1T1+n2T2+n3T3Three perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
An1T21+n2T22+n3T23n1T1+n2T2+n3T3Bn21T21+n22T22+n23T23n1T1+n2T2+n3T3CT1+T2+T33Dn1T1+n2T2+n3T3n1+n2+n3Two perfect gases at absolute temperature T1andT2 are mixed. There is no loss of energy. The masses of the molecules are m1andm2. The number of molecules in the gases are n1andn2. The temperature of the mixture is
AT1+T2BT1+T22Cn1T1+n2T2n1+n2DNone of these
Two perfect gases having masses m1andm2 at temperatures T1andT2 respectively are mixed without any loss of energy. If the molecular weights of the gas are M1andM2 respectively, then the final temperature of the mixture is
View SolutionTwo perifect gases at absolute temperatures T1andT2 are mixed. The absolute temperature of the mixture is T. there is no loss of energy.If m1andm2 are masses of molecules and n1andn2 are number of molecules, then
View Solution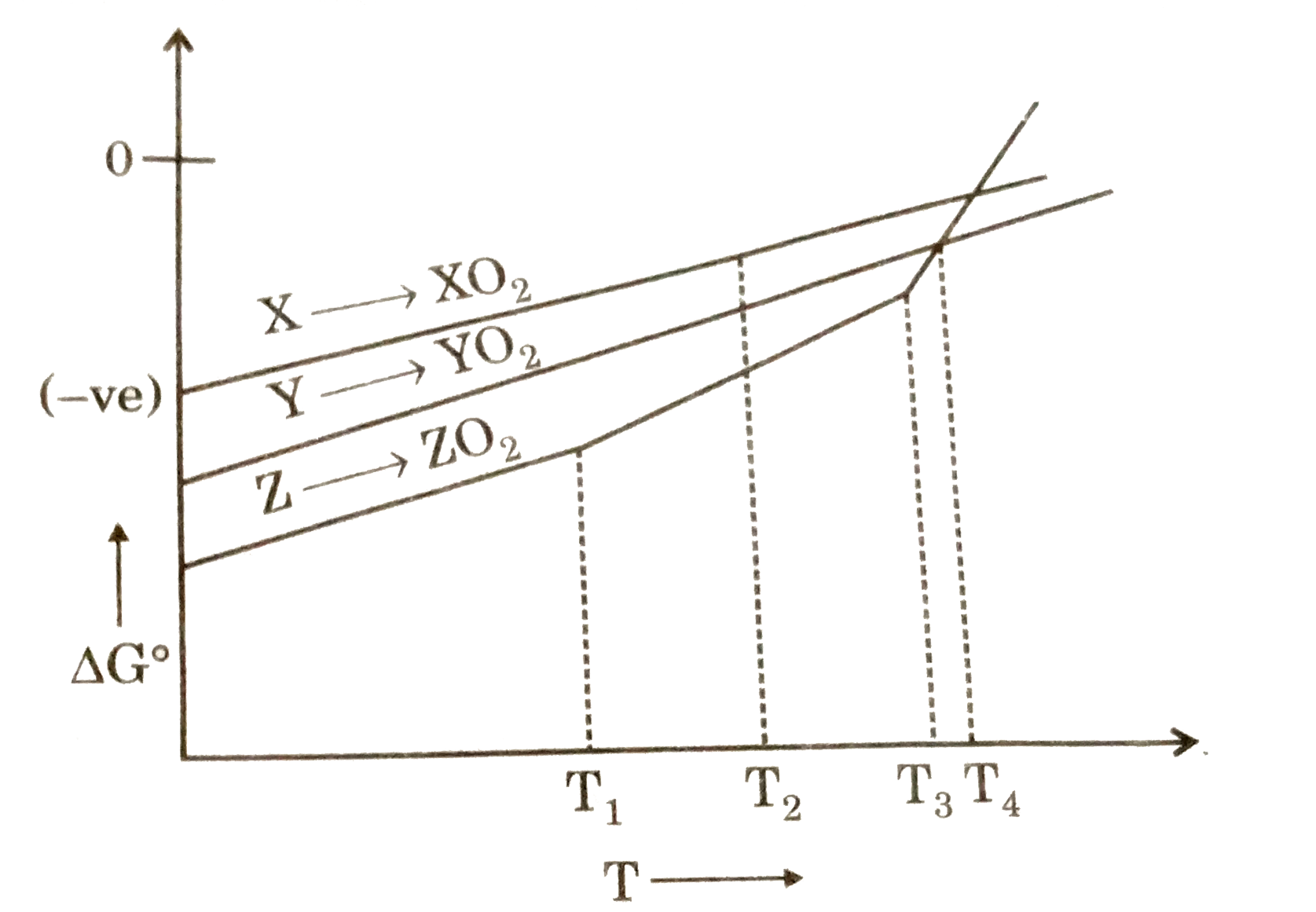
Temperature T1andT3 represents respectively:
View SolutionTwo polyatomic ideal gases are mixed together temperatures T1 and T2, number of molecules N1 and N2, mass of particles m1 and m2, degrees of freedom f1 and f2 find final temperatures of mixtures.
View SolutionThree liquids with masses m1,m2,m3 are throughly mixed. If their specific heats are c1,c2,c3 and their temperature T1,T2,T3, respectively, then the temperature of the mixture is
View Solution
