Two identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length zof0.06π meter and spring spring constant5 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.
The correct Answer is:A, B, C, D
(i) As both the balls displaced by θπ/6
radian with espect to the diameter PQ of the circle and released from rest. It results into compression of spring in upper segment and an equal elongation of spring in lower segment. Let it x. Pband QA denote x in the figure.
(##JMA_CHMO_C10_028_S01##)
Compression =Rtheta= elongation =x<br>∴Forceexertedbyeachspr∈goneachball=2kx
:. Total force on each ball due to two spring 4kx
:. Restoring torque about origin =O=−(4kx)R
:. tau=-4k (Rtheta) R, where theta =Anfular displacement
or τ=−4kR2θ
Since torque (tau) is proprtional to theta, each ball executes angular SHM about the centreO.
Again, τ=−4kR2θ
or lα=−4kR2θ where alpha=angular acceleration<br>or(mR^(2))alpha=-4kR^(2)theta or alpha=-((4k)/m)theta<br>∴Frequencyf=1/2_(pi)sqrtalpha/theta<br>∴Frequency of each ball=1/2_(pi)sqrt(4k)/m<br>=1/2_(pi)sqrt(4xx0. 1)/(0.1)=1/(pi)sec^(-1)<br>(ii)Letvelocityatthemeanpositionbevmax
Loss in elastic potential energy=Gain in kinetic energy<br>[1/2K(2R(pi)/2)]<br>2[1/1xx0.1(0.02pi)^(2)]
=3.95×10−4J.
Topper's Solved these Questions
Similar Questions
Two identical balls AandB eavh of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced bu an angle θ=π/6 dadius withrespect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.

View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
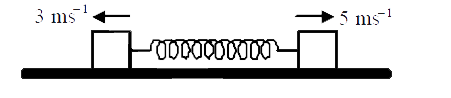
Choose the correct statement -
View Solution
Knowledge Check
Two identical massless springs A and B consist spring constant kA and kB respectively. Then :
Ait they are compressed by same force, work done on A is more expanded when kA>kBBif they are compressed by same amount, work done on A is more expanded when kA<kBCif they are compressed by same amount, work done on A is more expanded when kA>kBDboth (1) and (2) are correctA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkTwo bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?
 A(F/M)−aBaC−aD(F/M)
A(F/M)−aBaC−aD(F/M)
Two masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B wil be :-

View SolutionTwo identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is

View SolutionTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
View SolutionTwo masses of 1kg and 5kg are attached to the ends of a massless string passing over a pulley of negligible weight. The pulley itself is attached to a light spring balance as shown in figure. The masses start moving during this interval, the reading of spring balance will be:

View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View Solution
