Question

The air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency $440Hz$. The speed of sound in air is $330m{s}^{-1}$. End corrections may be naglected. Let $P_0$ denote the mean pressure at any point in the pipe, and $\Delta P$ the maximum amplitude of pressure variation.
(a) Find the length $L$ of the air column.
(b) What is the amplitude of pressure variation at the middle of the column?
( c ) What are the maximum and minimum pressures at the open end of the pipe?
(d) What are the maximum and minimum pressures at the closed end of the pipe?

Answer

A::B::C::D

Explanation

(a) For second overtone as shown,
`(5lambda)/(4) = l` :. `lambda = (4l)/(5)`
Also, `v = vlambda`
rArr `330 = 440 xx (4l)/(5)` rArr `l = (15)/(16)m`.

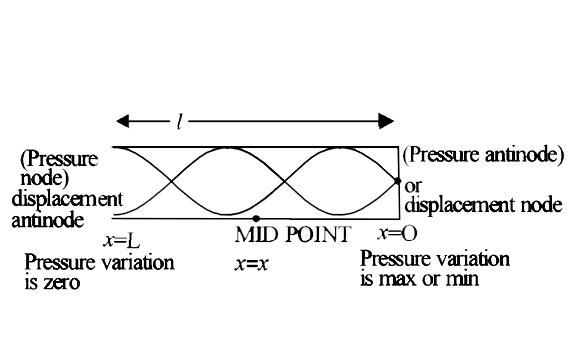
(b) KEY CONCEPT : At any position `x`, the pressure is given by
`DeltaP = DeltaP_(0) cos kx cos omegat`
For `x = (15)/(2 xx 16) = (15)/(32)m` (mid point)
`Amplitude = DeltaP_(0) cos[(2pi)/((330//440)) xx (15)/(32)] = (DeltaP_(0))/sqrt(2)`
( c ) At open end of pipe, pressure is always same i.e. equal to mean pressure `because` `DeltaP = 0, P_(max) = P_(min) = P_(0)`
(d) At the closed end :
Maximum pressure ` = P_(0) + DeltaP_(0)`
Minimum Pressure `= P_(0) - DeltaP_(0)`