A Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be

A

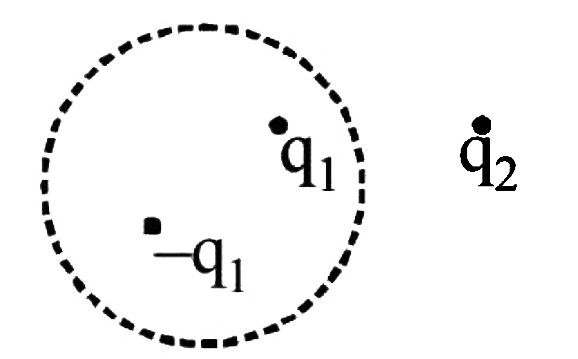
(a) due to $q_{1}$ and $q_{2}$ only

B

(b) due to $q_{2}$ only

C

(c) $z e r o$

D

(d) due to all

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

The flux through the Gausisan surface is due to the charges inisde the Gausisan surface. But the electric field on the Gausisan surface will be due to the charges present in the isde the Gausisan surface and outisde it. It will be due to all the charges.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A Gaussian surface encloses a proton p. The electric field at any point on the surface is $\to €$ . The flux linked with the Gaussian surface is $ϕ$ .
STATEMENT-1 $:$ When an electron is kept close to this system outside the Gaussian surface, the flux linked with the surface would change.
and
STATEMENT-2 $:$ The presence of electron will alterthe electric field on the gaussian surface.
AStatement-1 is True, Statement-2 is True, Statement -2 is a correct explanation for Statement-1
BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
CStatement-1 is True, Statement -2 is False
DStatement-1 is False, Statement-2 is True.
Question 2 - Select One
Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

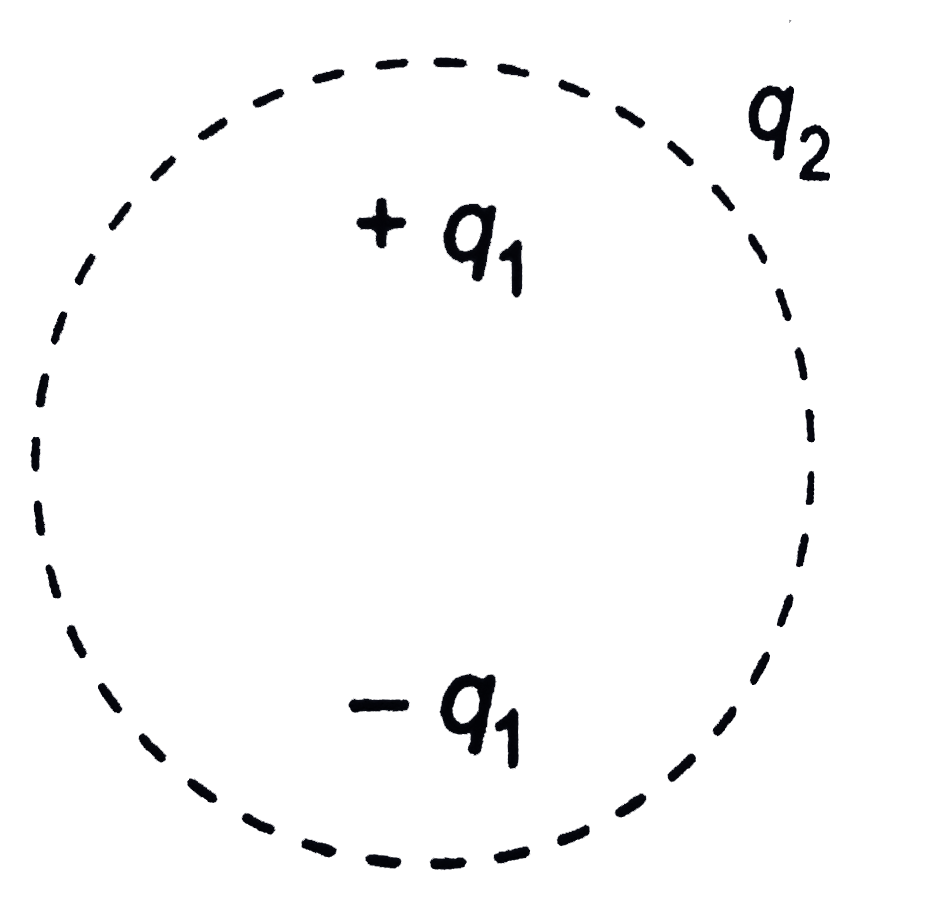A $q_{2}$
Bonly the positive charges
Call the charges
D $+ q_{1}$ and $- q_{1}$
Question 3 - Select One
If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
A0
Bsame at all places
Cdepends upon the location of points
Dinfinite

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-ELECTROSTATICS-Comprehension Based Questions

Home
Ask Doubt
Profile