A thin fixed of radius 1 metre has a positive charge 1×10−5 coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of 1×10−6 coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
The correct Answer is:B, C
KEY CONCEPT: The electric field due a uniformly charged ring of radius r at a point distant x from its center on its axis is given by
E=kQx(r2+x2)3/2
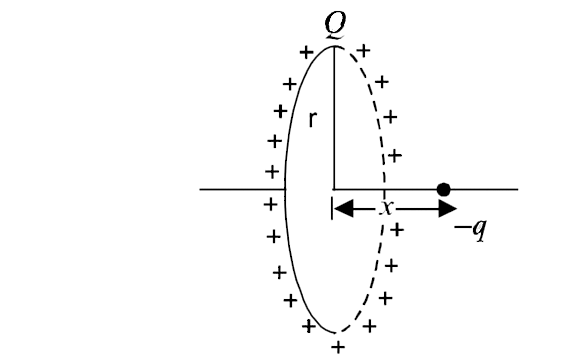
r=1m
Q=10−5C
mass of particle m=0.9×10−3kg
charge on particle q=−10−6C
∴ Force on the negative charge q will be F=qE
∴ F=−kQq(r2+x2)3/2×x or, mA=−kQq(r2+x2)3/2×x
or, A=−kQqm(r2+x2)3/2×x
For x<<r A=−kQqr3×x
⇒ The motion is simple harmonic in nature.
Comparing the above equation with A=−ω2x we get
∴ ω2=kQqmr3 or ω=√kQqmr3
∴ 2πT=√kQqmr3⇒T=2π√mr3kQq
T=2×3.14[0.19×10−3×139×109×10−5×10−6]1/2
=6.28[0.01]1/2=6.28[0.1]
T=0.628sec
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
A thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.

View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View Solution
Knowledge Check
A non conducting spherical shell of diameter 10 cm has a charge of 1.6×10−4C. A charge of 20 C is placed at a distance of 10 cm from its centre, then force between them will be :-
A4×109NB16×1015NC3×109ND6×10−9NA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
A27 VB13.5 VC54 VD45.5 VThe electronic charge is 1.6×10−19 coulomb. If a body carries a negative charge of 9.6×10−10 coulombs, what is the number of excess electrons on the body?
A6×109B1/6×10−29C6×1029D6×1029
Mass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View SolutionA charge +Q is uniformly distributed over a thin ring of a radius R. Find the velocity of a negative point charge -Q at the moment it passes through the centre of the ring if it was initially at rest at infinity on the axis of the ring. The mass of the charge-Q is equal to m.
View SolutionA conducting ring of radius 40 cm has a charge of 5×10−9 C uniformly distributed over it. Calculate the electric field intensity at a point P, 40 cm away from the centre on the axis of the ring.
View SolutionA charge +Q is uniformluy distributed over a thin ring with radus R.a negative point charge -Q and mass m starts from rest at a pont far away from the centre of the ring and moves towardsn then centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View Solution
