Two parallel plate capacitors A and B have the same separation $d = 8.85 \times 10^{- 4} m$ between the plates. The plate area of A and B are $0.04 m^{2}$ and $0.02 m^{2}$ respectively. A slab of dielectric constant (relative permittivity) $K = 9$ has dimensions such that it can exactly fill the space between the plates of capacitor B.

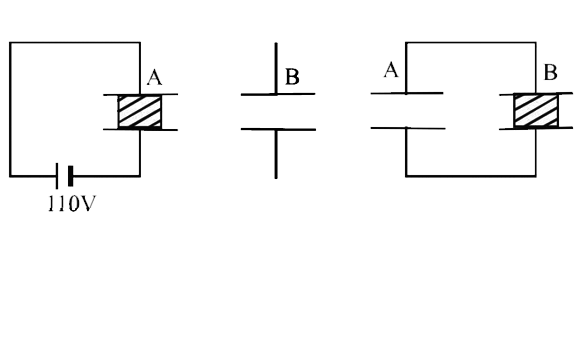
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

(i) The combined capacitance is

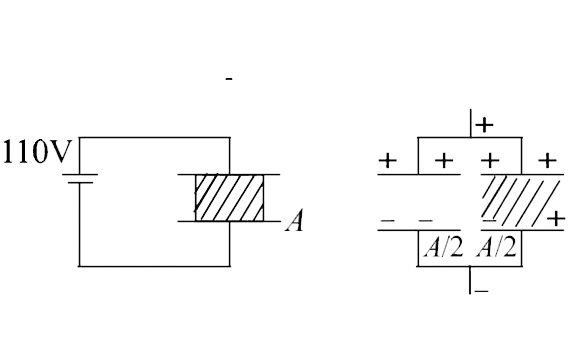
$C = C_{1} + C_{2}$
$= \frac{(A / 2) ε_{0}}{d} + \frac{(A / 2) ε_{0} ε_{r}}{d} = \frac{A}{2} \frac{ε_{0}}{d} [1 + ε_{r}]$
$= \frac{0.4 \times 8.85 \times 10^{- (12)}}{2 \times 8.85 \times 10^{- 4}} [1 + 9] = 2 \times 10^{- 9} F$
$∴$ Energy stored $= \frac{1}{2} C V^{2} = \frac{1}{2} \times 2 \times 10^{- 9} \times {(110)}^{2}$
$= 1.21 \times 10^{- 5} J$
(ii) Work done in removing the dielectric slab = (Energy stored in capacitor without dielectric)-(Energy stored in capacitor with dielectric).
$∴$ $W = \frac{q^{2}}{2 C^{'}} - \frac{q^{2}}{2 C}$ Here, $C = 2 \times 10^{- 9} F$ ,
$C^{'} = \frac{A ε_{0}}{d} = \frac{0.04 \times 8.85 \times 10^{- 14}}{8.85 \times 10^{- 4}} = 0.4 \times 10^{- 9} F$
$q = C V = 2 \times 10^{- 9} \times 110 = 2.2 \times 10^{- 7} C$
$∴$ $W = \frac{{(2.2 \times 10^{- 7})}^{2}}{2} [\frac{1}{0.4 \times 10^{- 9}} - \frac{1}{2 \times 10^{- 9}}]$
$= 4.84 \times 10^{- 5} J$
(iii) The capacitance of $B = \frac{ε_{0} ε_{r} A_{B}}{d}$
$= \frac{8.85 \times 10^{- 12} \times 9 \times 0.2}{8.85 \times 10^{- 4}}$
$C_{B} = 1.8 \times 10^{- 9} F$
The charge on A, $q_{A} = 2.2 \times 10^{- 7} C$ gets distributed into two parts.
$∴$ $q_{1} + q_{2} = 2.2 \times 10^{- 7} C$
also the potential difference across A=p.d. across B
$\frac{q_{1}}{C_{A}} = \frac{q_{2}}{C_{B}}$
$\Rightarrow q_{1} = \frac{C_{A}}{C_{B}} q_{2} = (\frac{0.4 \times 10^{- 9}}{1.8 \times 10^{- 9}} q_{2} = 0.22 q_{2}$
$∴$ $0.22 q_{2} + q_{2} = 2.2 \times 10^{- 7}$
$\Rightarrow q_{2} = \frac{2.2}{1.22} \times 10^{- 7} = 1.8 \times 10^{- 7} C$
$\Rightarrow q_{1} = 0.4 \times 10^{- 7} C$
Total energy stored $= \frac{q_{1}^{2}}{2 C_{A}} + \frac{q_{2}^{2}}{2 C_{B}}$
$= \frac{0.4 \times 0.4 \times 10^{- 14}}{2 \times 0.4 \times 10^{- 9}} + \frac{1.8 \times 1.8 \times 10^{- 14}}{2 \times 1.8 \times 10^{- 8}}$
$= 0.2 \times 10^{- 5} + 0.9 \times 10^{- 5} = 1.1 \times 10^{- 5} J$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zero
Bremains the same
Cdecreases
Dincreases
Question 2 - Select One
A parallel plate capacitor having capacitance C farad is connected with a battery of emf V volts. Keeping the capacitor cannected with the battery, a dielectric slab of dielectric constant K is inserted between the plates. The dimensions of the slab are such that it fills the space between the capacitor plates. Then,
Acharge the capacitor plates remains the same
Bcharge on the plates increases K times
Cpotential difference between the plates decreases to $V / K$
Dall of these
Question 3 - Select One
Separation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-

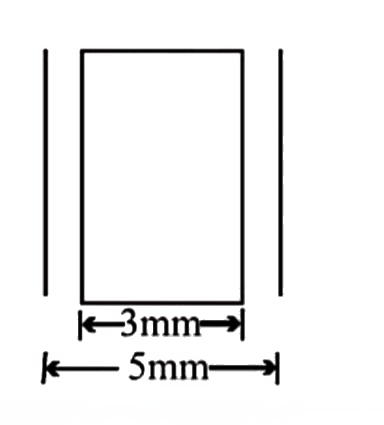A18.5V
B13.5V
C11.5V
D6.5V

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-ELECTROSTATICS-Comprehension Based Questions

Home
Ask Doubt
Profile