If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
(a) (ϕ2−ϕ1)εo
(b) (ϕ1+ϕ2)/εo
(c) (ϕ2−ϕ1)/εo
(d) (ϕ1+ϕ2)εo
The correct Answer is:A
To find the electric charge inside an enclosed surface when the electric flux entering and leaving the surface are given as ϕ1 and ϕ2 respectively, we can use Gauss's law.
1. Understand the Concept of Electric Flux:
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which it passes, and it is given by the formula:
Φ=E⋅A
2. Apply Gauss's Law:
According to Gauss's law, the net electric flux (Φnet) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ϵ0):
Φnet=Qϵ0
3. Calculate the Net Electric Flux:
The net electric flux through the surface can be calculated as the difference between the flux leaving the surface (ϕ2) and the flux entering the surface (ϕ1):
Φnet=ϕ2−ϕ1
4. Relate the Net Electric Flux to Charge:
Substituting the expression for net electric flux into Gauss's law gives:
ϕ2−ϕ1=Qϵ0
5. Solve for the Enclosed Charge Q:
Rearranging the equation to solve for the charge Q gives:
Q=(ϕ2−ϕ1)⋅ϵ0
Final Answer:
Thus, the electric charge inside the surface is:
Q=(ϕ2−ϕ1)⋅ϵ0
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which it passes, and it is given by the formula:
Φ=E⋅A
According to Gauss's law, the net electric flux (Φnet) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ϵ0):
Φnet=Qϵ0
The net electric flux through the surface can be calculated as the difference between the flux leaving the surface (ϕ2) and the flux entering the surface (ϕ1):
Φnet=ϕ2−ϕ1
Substituting the expression for net electric flux into Gauss's law gives:
ϕ2−ϕ1=Qϵ0
Rearranging the equation to solve for the charge Q gives:
Q=(ϕ2−ϕ1)⋅ϵ0
Thus, the electric charge inside the surface is:
Q=(ϕ2−ϕ1)⋅ϵ0
Topper's Solved these Questions
- ELECTROSTATICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROSTATICSExercise:Subjective Problems
Explore 2 Videos
- ELECTROSTATICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROSTATICSExercise:Comprehension Based Questions
Explore 2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:JEE Main And Advanced
Explore 107 Videos
- MODERN PHYSICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:MODERN PHYSICSExercise:MCQ (One Correct Answer
Explore 1 Video
Similar Questions
Knowledge Check
If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2 then the electric charge inside the surface will he
A(ϕ+ϕ2)ε0B(ϕ2−ϕ1)ε0C(ϕ1−ϕ2)ε0D(−ϕ1−ϕ2)ε0If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
Aϕ3−ϕ1εnBϕ2+ϕ1εnC(ϕ1−ϕ3)εnDεn(ϕ2−ϕ1)If the electric flux entering and leaving an enclosed surface are ϕ1andϕ2 respectively, then the electric charge present within the surface is
A1∈0(ϕ1+ϕ2)B1∈0(ϕ2−ϕ1)C∈0(ϕ1+ϕ2)D∈0(ϕ2−ϕ1)
Electric flux through a closed surface in free space enclosing a charge q is
View SolutionThe electric flux through the surface
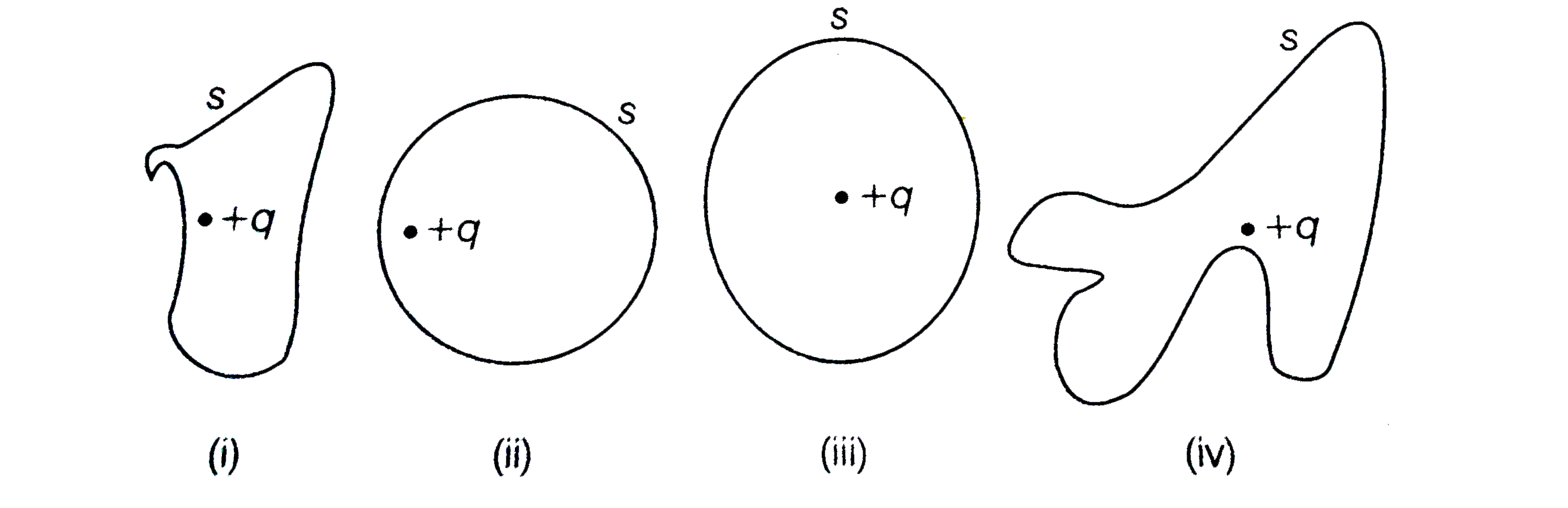
View SolutionThe electric flux through the surface

View SolutionIf the electric flux entering and leaving a closed surface are 6×106 and 9×106 SI units respectively, then the net charge inside the surface of permittivity of free space ε0 is
View SolutionIf ϕ1andϕ2 are normal of flux entering and leaving an enclosed surface. Electric flux inside the surface will be
View Solution