A charge particle 'q' is shot towards another charged particle 'Q' which is fixed, with a speed 'v'. It approaches 'Q' upto a closest distance r and then returns. If q were given a speed of '2v' the closest distances of approach would be
(a) r/2
(b) 2/r
(c) r
(d) r/4
The correct Answer is:D
To solve the problem, we need to apply the principle of conservation of energy. The total mechanical energy of the system (kinetic energy + potential energy) remains constant as the charged particle approaches the fixed charge.
1. Initial Conditions:
- A charge particle q is shot towards a fixed charge Q with an initial speed v.
- The closest distance of approach is r.
2. Energy at Closest Distance:
- The initial kinetic energy KE1 when the particle is shot is given by:
KE1=12mv2
- The potential energy PE at the closest distance r is given by:
PE=kQqr
- By conservation of energy, we have:
KE1=PE
- Therefore, we can write:
12mv2=kQqr(1)
3. New Conditions with Speed 2v:
- Now, if the charge particle q is given a speed of 2v, the new kinetic energy KE2 becomes:
KE2=12m(2v)2=12m⋅4v2=2mv2
- Let the new closest distance of approach be r′. The potential energy at this distance is:
PE′=kQqr′
- By conservation of energy, we have:
KE2=PE′
- Therefore, we can write:
2mv2=kQqr′(2)
4. Relating the Two Equations:
- From equation (1), we know:
kQqr=12mv2
- Substituting this into equation (2):
2mv2=4⋅kQqr
- Rearranging gives:
kQqr′=4⋅kQqr
- This implies:
r′=r4
5. Conclusion:
- The closest distance of approach when the charge particle q is given a speed of 2v is:
r′=r4
Final Answer:
The closest distance of approach when the speed is 2v is r4.
---
- A charge particle q is shot towards a fixed charge Q with an initial speed v.
- The closest distance of approach is r.
- The initial kinetic energy KE1 when the particle is shot is given by:
KE1=12mv2
- The potential energy PE at the closest distance r is given by:
PE=kQqr
- By conservation of energy, we have:
KE1=PE
- Therefore, we can write:
12mv2=kQqr(1)
- Now, if the charge particle q is given a speed of 2v, the new kinetic energy KE2 becomes:
KE2=12m(2v)2=12m⋅4v2=2mv2
- Let the new closest distance of approach be r′. The potential energy at this distance is:
PE′=kQqr′
- By conservation of energy, we have:
KE2=PE′
- Therefore, we can write:
2mv2=kQqr′(2)
- From equation (1), we know:
kQqr=12mv2
- Substituting this into equation (2):
2mv2=4⋅kQqr
- Rearranging gives:
kQqr′=4⋅kQqr
- This implies:
r′=r4
- The closest distance of approach when the charge particle q is given a speed of 2v is:
r′=r4
The closest distance of approach when the speed is 2v is r4.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
A particle of mass m, charge q>0 and initial kinetic energy K is projected from infinity towards a heavy nucleus of charge Q assumed to have a fixed position.
(a) If the aim is perfect, how close to the centre of the nucleus is the particle when it comes instantaneously to rest ?
(b) With a particular imperfect aim, the particle's closest approach to nucleus is twicw the distance determined in (a). Determine speed of particle at the closest distance of approach.
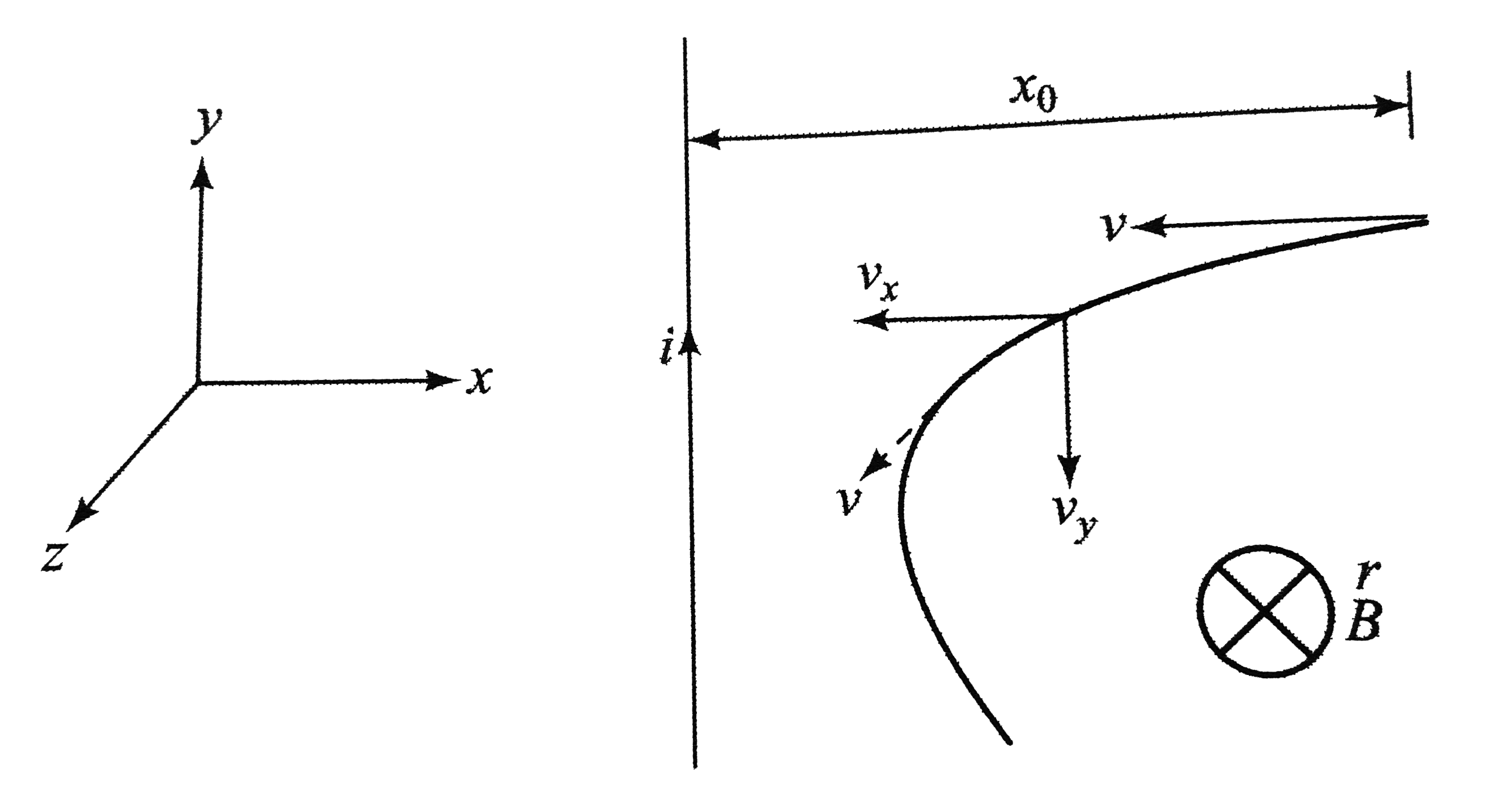
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View Solution
Knowledge Check
A charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distance of approach would be
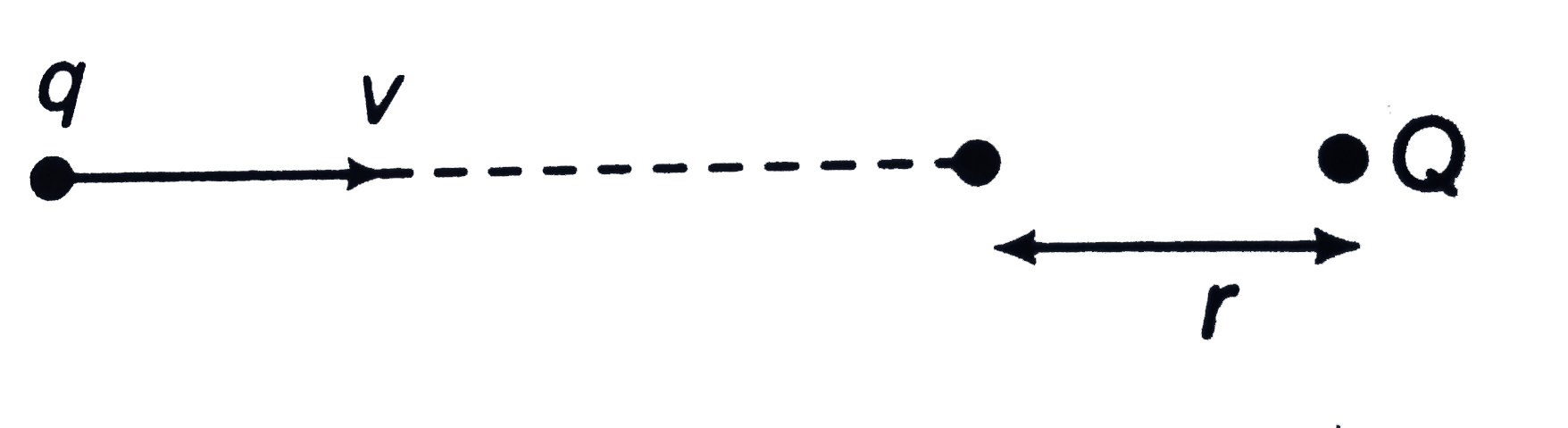 ArB2rCr/2Dr/4
ArB2rCr/2Dr/4A charged particle of charge 'Q' is held fixed and another charged particle of mass 'm' and charge 'q' (of the same sign) is released from a distance 'r'. The impulse of the force exerted by the external agent on the fixed charge by the time distance between 'Q' and 'q' becomes 2r is
A√Qq/4π∈0mrB√Qqm/4π∈0rC0Dcannot determineTwo identical particles of mass m carry a charge Q, each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be .
A14πQ2mvB14πɛ04Q2mv2C14πɛ02Q2mv2D14πɛ03Q2mv2
Q:6DTQ Two particles of mass m and 2m carry a charge q each.Initially the heavier particle is at rest on a smooth horizontal plane and the other is projected along the plane directly towards the first from a distance d with speed u.If the closest distance of approach is 3q2dnq2+4πɛ0u2d then find the value of n .
View SolutionA charge "Q" of mass "m" is at rest on a smooth horizontal plane.Another identical particle is projected with a velocity v towards it from long distance then
View SolutionTwo particles of mass m and 2m carry a charge q each.Initially the heavier particle is at rest on a smooth horizontal plane and the other is projected along the plane directly towards the first from a distance d with speed u .If the closest distance of approach is 3q2dnq2+4πe0u2d then find the value of n .
View SolutionFigure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
View SolutionA particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :

View Solution
