Assume that an electric field →E=30x2ˆj exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
(a) 120J/C
(b) −120J/C
(c) −80J/C
(d) 80J/C
The correct Answer is:C
To find the potential difference VA−VO where VO is the potential at the origin and VA is the potential at x=2m, we start with the given electric field:
→E=30x2^j
Step 1: Relate Electric Field to Potential
The relationship between electric field →E and electric potential V is given by:
→E=−dVdx
Step 2: Set Up the Integral
To find the potential difference VA−VO, we can rearrange the equation:
VA−VO=−∫20→E⋅d→x
Since the electric field is in the ^j direction, we need to consider the y component of the field. However, since the field is only in the y direction and we are moving in the x direction, we can express this as:
VA−VO=−∫2030x2dx
Step 3: Calculate the Integral
Now we compute the integral:
VA−VO=−30∫20x2dx
Calculating the integral:
∫x2dx=x33
So we evaluate it from 0 to 2:
∫20x2dx=(x33)20=233−033=83
Step 4: Substitute Back into the Equation
Now substituting back into the equation for potential difference:
VA−VO=−30(83)
Calculating this gives:
VA−VO=−80
Final Result
Thus, the potential difference VA−VO is:
VA−VO=−80J/Cor−80V
The relationship between electric field →E and electric potential V is given by:
To find the potential difference VA−VO, we can rearrange the equation:
Now we compute the integral:
Now substituting back into the equation for potential difference:
Thus, the potential difference VA−VO is:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
Knowledge Check
Assume that an electric field →E=30x2ˆi exists in space. Then the potentail differences VA−V0 where V0 is the potential at the origin and VA, the potebntail at x=2m is
A−80VB80VC120VD−120V
An electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionAn electric field →E=(25ˆi+30ˆj)NC−1 exists in a region of space.If the potential at the origin is taken to be zero then the potential at x=2 m y=2 m is :?
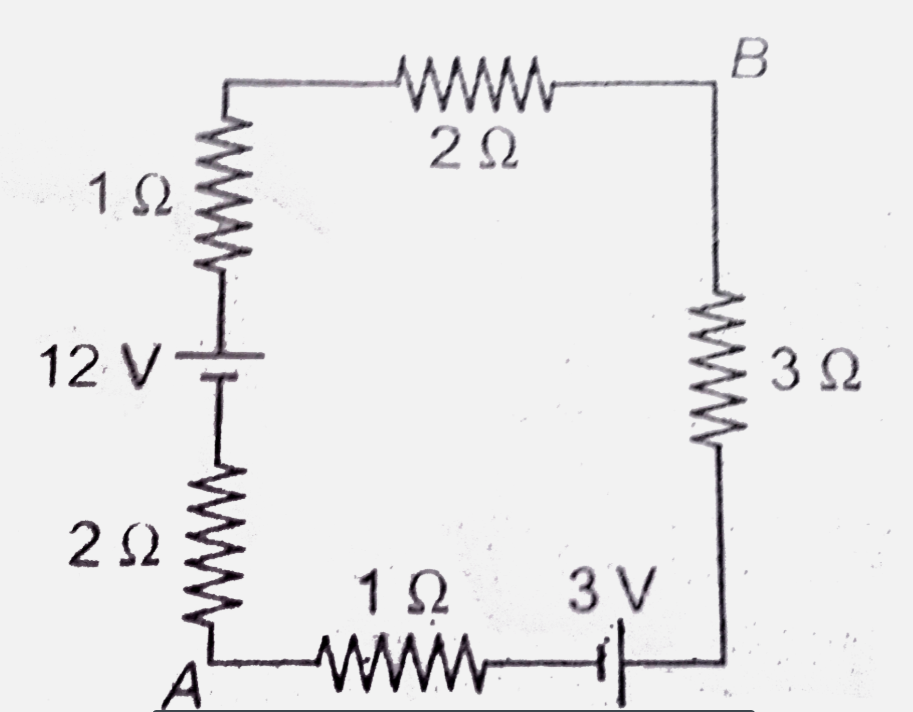
View SolutionPotential difference VB−VA in the network shown is
View SolutionAn electric field →E=→IAx exists in the space, where A=10Vm−2. Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionAn electric field →E=ˆiCx exists in the space, where C = 10 V/m2 . Taking the potential at (10 m, 20 m ) to be zero, find the potential at the origin.
View SolutionAn electric field →E=(25ˆi+30ˆj)NC−1 exists in a region of space.If the potential at the origin is taken to be zero then the potential at x=2m y=2m is : (A) -110V (B) -140V (D) -120V -130V
View SolutionA uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View Solution