Two short bar magnets of length 1cm each have magnetic moments 1.20Am2and1.00Am2 respectively. They are placed on a horizontal table parallel to each other with their N poles pointing towards the south. They have a common magnetic equator and are separted by a distance of 20.0cm. The value of the resultant horizontal magnetic induction at the mid - point O of the line joining their centres is close to (Horizontal component of earths magnetic induction is 3.6×10.5Wh/m2
3.6×10.5Wh/m2
2.56×10.4Wh/m2
3.50×10.4Wh/m2
5.80×10.4Wh/m2
The correct Answer is:B
To solve the problem, we need to calculate the resultant magnetic induction at the midpoint O between the two bar magnets. Here are the steps to find the solution:
Step 1: Understand the Configuration
We have two bar magnets with magnetic moments M1=1.20Am2 and M2=1.00Am2. They are placed parallel to each other with their north poles pointing towards the south. The distance between the magnets is 20.0cm.
Step 2: Determine the Midpoint
The midpoint O is located halfway between the two magnets. Therefore, the distance from each magnet to the midpoint is:
R=20.0cm2=10.0cm=0.1m
Step 3: Calculate the Magnetic Field Due to Each Magnet
The magnetic field B at a distance R from a magnetic dipole is given by the formula:
B=μ04π⋅2MR3
where μ0=4π×10−7T m/A.
For Magnet 1:
Using M1=1.20Am2:
B1=4π×10−74π⋅2×1.20(0.1)3=10−7⋅2.40.001=2.4×10−4T
For Magnet 2:
Using M2=1.00Am2:
B2=4π×10−74π⋅2×1.00(0.1)3=10−7⋅2.00.001=2.0×10−4T
Step 4: Determine the Direction of the Magnetic Fields
Since both magnets have their north poles pointing towards the south, the magnetic field B1 from magnet 1 at point O will point towards the north (upward), and the magnetic field B2 from magnet 2 will also point towards the north (upward).
Step 5: Calculate the Resultant Magnetic Field
The resultant magnetic field Bnet at point O is the sum of the individual magnetic fields:
Bnet=B1+B2=2.4×10−4+2.0×10−4=4.4×10−4T
Step 6: Include the Earth's Magnetic Field
The horizontal component of the Earth's magnetic field is given as BH=3.6×10−5T. Since the Earth's magnetic field is also directed towards the north, we add it to the resultant magnetic field:
Btotal=Bnet+BH=4.4×10−4+3.6×10−5=4.76×10−4T
Step 7: Final Result
The resultant horizontal magnetic induction at the midpoint O is approximately:
Btotal≈4.76×10−4T or 4.76×10−4Wb/m2
We have two bar magnets with magnetic moments M1=1.20Am2 and M2=1.00Am2. They are placed parallel to each other with their north poles pointing towards the south. The distance between the magnets is 20.0cm.
The midpoint O is located halfway between the two magnets. Therefore, the distance from each magnet to the midpoint is:
R=20.0cm2=10.0cm=0.1m
The magnetic field B at a distance R from a magnetic dipole is given by the formula:
B=μ04π⋅2MR3
where μ0=4π×10−7T m/A.
Using M1=1.20Am2:
B1=4π×10−74π⋅2×1.20(0.1)3=10−7⋅2.40.001=2.4×10−4T
Using M2=1.00Am2:
B2=4π×10−74π⋅2×1.00(0.1)3=10−7⋅2.00.001=2.0×10−4T
Since both magnets have their north poles pointing towards the south, the magnetic field B1 from magnet 1 at point O will point towards the north (upward), and the magnetic field B2 from magnet 2 will also point towards the north (upward).
The resultant magnetic field Bnet at point O is the sum of the individual magnetic fields:
Bnet=B1+B2=2.4×10−4+2.0×10−4=4.4×10−4T
The horizontal component of the Earth's magnetic field is given as BH=3.6×10−5T. Since the Earth's magnetic field is also directed towards the north, we add it to the resultant magnetic field:
Btotal=Bnet+BH=4.4×10−4+3.6×10−5=4.76×10−4T
The resultant horizontal magnetic induction at the midpoint O is approximately:
Btotal≈4.76×10−4T or 4.76×10−4Wb/m2
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - MCQs(d )
1 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
- RAY AND WAVE OPTICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - RAY AND WAVE OPTICSEXERCISE - JEE Main And Advanced
209 Videos
Similar Questions
Calculate the magnetic field intensity at a distance of 20cm. from a pole of strength 40Am in air. Find the magnetic induction at the same point.
View SolutionTwo short magnets (1) and (2) of magnetic moments 2Am2 and 5Am2 respectively are placed along two lines drawn at 90∘ to each other as shown in figure. At the point of intersection of their axes, the magnitude of magnetic field is n×10−5T. What is n?
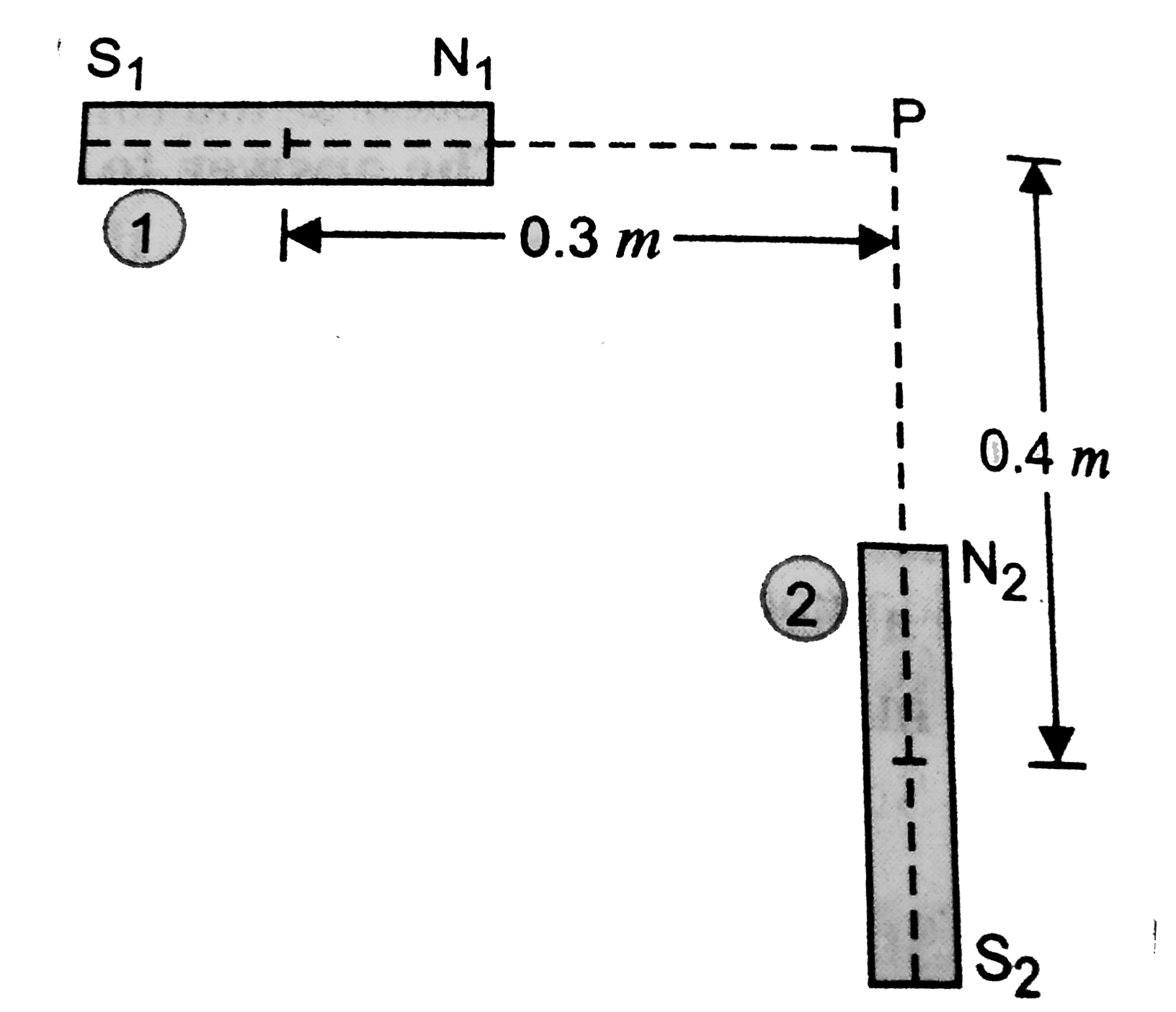
View Solution
Knowledge Check
The pole strength of a horse shoe magnet is 90Am and distance between the poles is 6cm. The magnetic induction at mid point of the line joining the poles is,
A10−2TBzeroC2×10−2TD10−4TTwo short bar magnets with magnetic moments 8Am2 and 27Am2 are placed 35cm apart along their common axial line with their like poles facing each other. The neutral point is
Amidway between themB21cm from weaker magnetC14cm from weaker magnetD27cm from weaker magnetA short bar magnet has a magnetic moment of 10 Am2.If its length is 10 cm,then the pole strength of the dipole is
A200 AmB100 AmC150 AmD50 Am
Two bar magnets of magnetic moments 12Am2 and 10Am2 are placed one over the other .First with their similar poles in contact after unlike poles in contact.The ratio of their resultant magnetic moments is
View SolutionThe pole strength of a bar magnet of magnetic moment 5Am2 and geometric length 6 cm is
View SolutionTwo identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
View SolutionTwo identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
View SolutionTwo short bar magnets of magnetic moments 0.1245Am2 and 0.512Am2 are placed with their like poles facing each other. If the distance between the centres of the magnet is 0.26m. The distance of neutral point from the weaker magnet is
View Solution
