In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
(Bπrω)22R
(Bπr2ω)28R
Bπr2ω2R
(Bπrω2)28R
The correct Answer is:B
To solve the problem, we need to determine the mean power generated per period of rotation for a wire in the form of a semicircle rotating in a uniform magnetic field. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a semicircular wire of radius r rotating about its diameter with an angular frequency ω in a uniform magnetic field B. The total resistance of the circuit is R.
Step 2: Determine the Area of the Semicircle
The area A of the semicircular wire can be calculated using the formula:
A=12πr2
Step 3: Calculate the Magnetic Flux
The magnetic flux Φ through the semicircular area when it rotates can be expressed as:
Φ=B⋅A⋅cos(θ)
where θ is the angle between the magnetic field and the normal to the area. As the wire rotates, θ changes with time as θ=ωt.
Thus, the magnetic flux becomes:
Φ(t)=B⋅(12πr2)⋅cos(ωt)
Step 4: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(B⋅12πr2cos(ωt))=B⋅12πr2⋅ωsin(ωt)
Step 5: Calculate the Current
Using Ohm's law, the current I in the circuit can be expressed as:
I=ER=B⋅12πr2⋅ωsin(ωt)R
Step 6: Determine the Peak Current
The peak current I0 can be defined as:
I0=B⋅12πr2⋅ωR
Step 7: Calculate the RMS Current
The root mean square (RMS) current Irms is given by:
Irms=I0√2=B⋅12πr2⋅ωR√2
Step 8: Calculate the Mean Power
The mean power P generated in the circuit is given by:
P=I2rms⋅R
Substituting the expression for Irms:
P=⎛⎝B⋅12πr2⋅ωR√2⎞⎠2⋅R
P=B2⋅14π2r4⋅ω22R
Step 9: Simplify the Expression
This simplifies to:
P=B2⋅π2r4⋅ω28R
Final Result
Thus, the mean power generated per period of rotation is:
P=B2⋅π2r4⋅ω28R
We have a semicircular wire of radius r rotating about its diameter with an angular frequency ω in a uniform magnetic field B. The total resistance of the circuit is R.
The area A of the semicircular wire can be calculated using the formula:
A=12πr2
The magnetic flux Φ through the semicircular area when it rotates can be expressed as:
Φ=B⋅A⋅cos(θ)
where θ is the angle between the magnetic field and the normal to the area. As the wire rotates, θ changes with time as θ=ωt.
Φ(t)=B⋅(12πr2)⋅cos(ωt)
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(B⋅12πr2cos(ωt))=B⋅12πr2⋅ωsin(ωt)
Using Ohm's law, the current I in the circuit can be expressed as:
I=ER=B⋅12πr2⋅ωsin(ωt)R
The peak current I0 can be defined as:
I0=B⋅12πr2⋅ωR
The root mean square (RMS) current Irms is given by:
Irms=I0√2=B⋅12πr2⋅ωR√2
The mean power P generated in the circuit is given by:
P=I2rms⋅R
Substituting the expression for Irms:
P=⎛⎝B⋅12πr2⋅ωR√2⎞⎠2⋅R
P=B2⋅14π2r4⋅ω22R
This simplifies to:
P=B2⋅π2r4⋅ω28R
Thus, the mean power generated per period of rotation is:
P=B2⋅π2r4⋅ω28R
Topper's Solved these Questions
Similar Questions
A wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
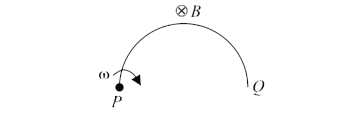
View SolutionA wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
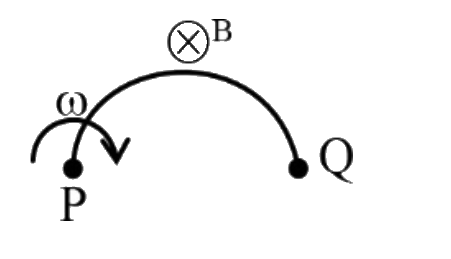
View Solution
Knowledge Check
In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
A(πBr2ω)28RBπBrω28RC(πBrω)28RD0A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
AMω2LBMω2L8CMω2L4DMω2L2
A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionCalculate the work that has to be done to stop an iron sphere of radius R rotating about its diameter with an angular velocity ω.
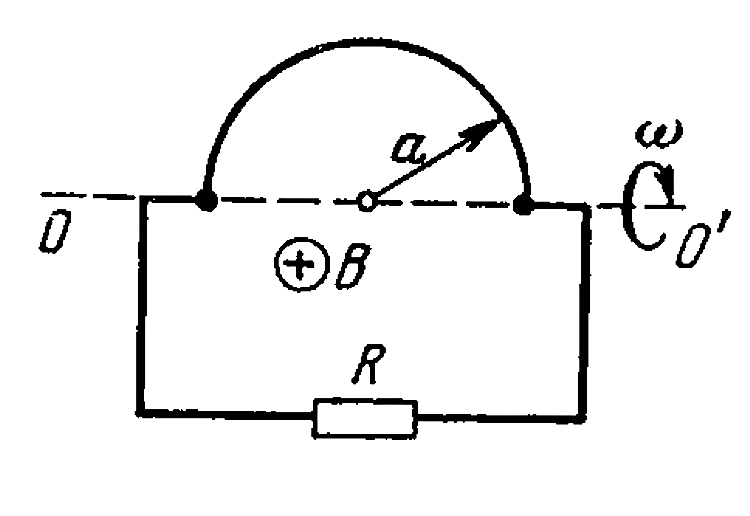
View SolutionA wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA rectangular coil of single trun, having area A , rotates in a uniform magnetic field B with an angular velocity ω about an axis prependicular to the field. If initially the plane of the coil is perpendicular to the field, then the average induced emf when it has rotate through 90∘ is
View Solution
