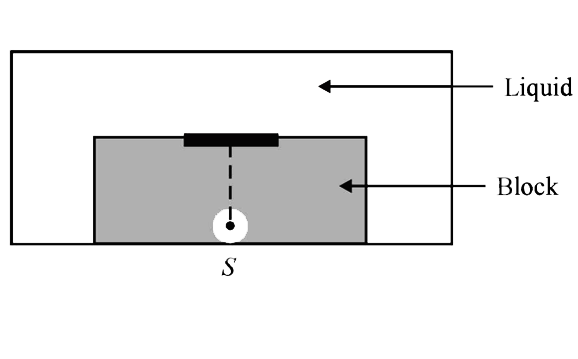
A point source S is placed at the bottom of a tranparent block of height 10mm and refractive index 2.72. It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54 mm on the top of the block. The refractive index of the liquid is
1.21
1.3
1.36
1.42
The correct Answer is:C
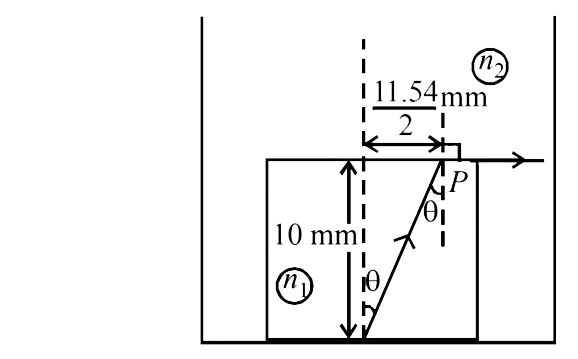
Applying Snell's law at point P
n1sinθ=n2sin90degree
∵ n2=2.72×11.542√(10)2+(11.542)2
∵ n2=1.36
Topper's Solved these Questions
Similar Questions
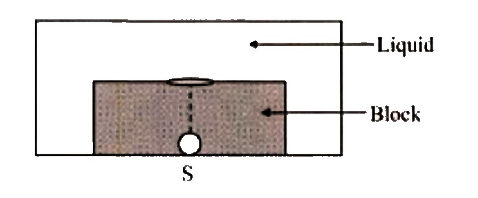
A point source S is placed at the bottom of a 12 mm high transparent block of diamond ( refractive index = 2.4 ) . The block is immersed in an optically rarer liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter 18 mm on the top of the block. What is the refractive index of the liquid ?
 View Solution
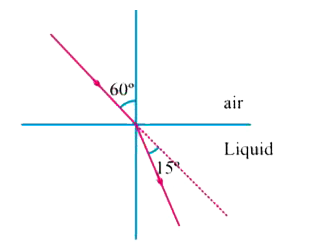
View SolutionA light ray passes from air into a liquid as shown in figure. Find refractive index of liquid.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point source S is placed at the bottom of a transparent block of height 10mm and refractive index 2.72. It is immersed in a lower refractive index liquid as shwon in Fig. I tis found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54mm on the top of the block. The refractive index of the liquid is
 A1.21B1.30C1.36D1.42
A1.21B1.30C1.36D1.42 - Question 2 - Select One
A spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
A10 cmB8 cmC6 cmD4 cm - Question 3 - Select One
A ray of light is incident normally on the prism (μ=32) immersed in a liquid as shown in the figure. The largest value for the angle α so that ray is totally reflected at the face AC is 30∘. The refractive index of the given liquid is
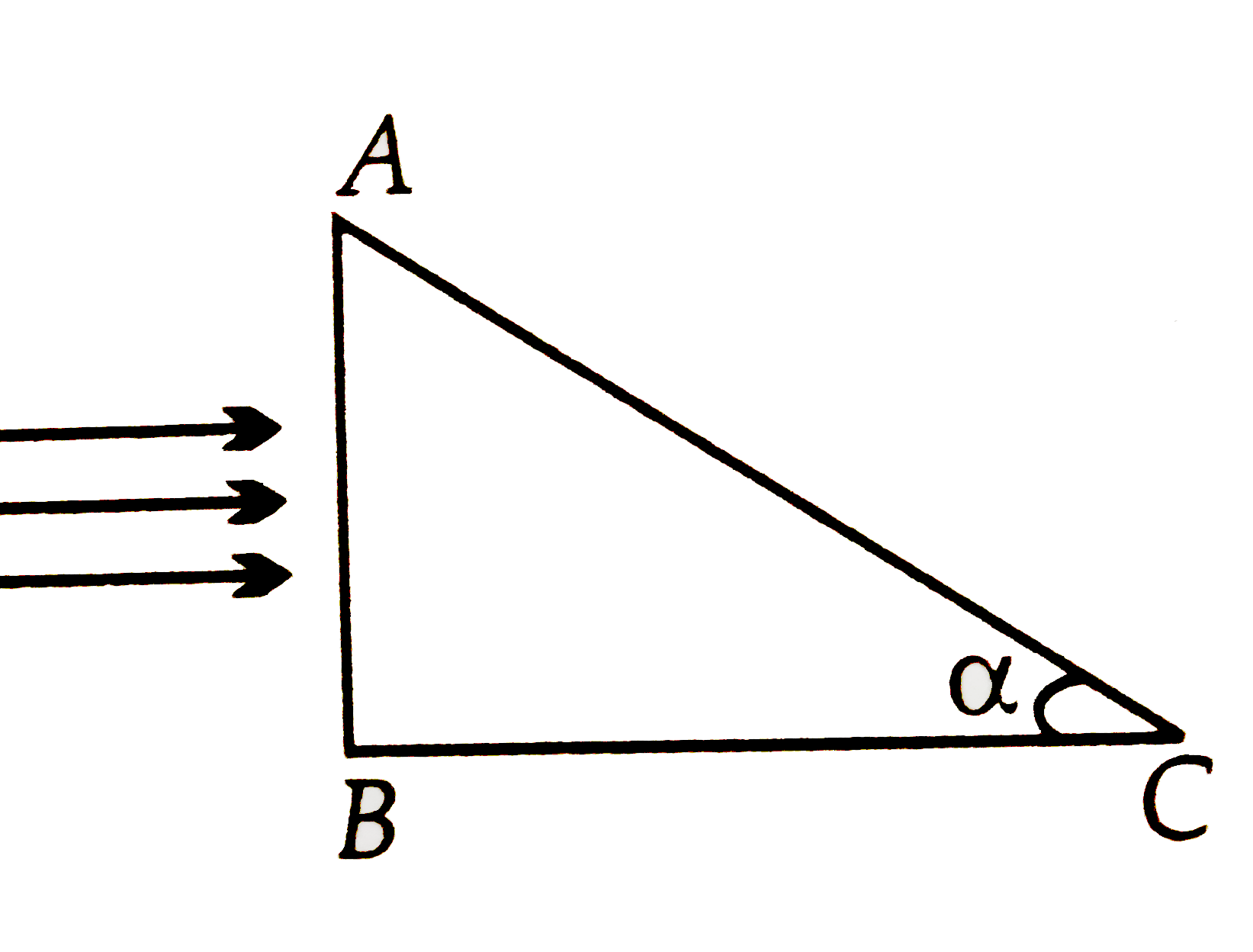 A√32B34C43D3√34
A√32B34C43D3√34
A point light source is attached to the base of an empty trough. A transparent liquid of refractive index 1.35 is filled in the trough to a height of 50 cm. Calculate the total area on the surface of the liquid through which light will emerge.
View SolutionThe speed of the yellow light in a certain liquid is2.4x108ms−1. Find the refractive index of the liquid.
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
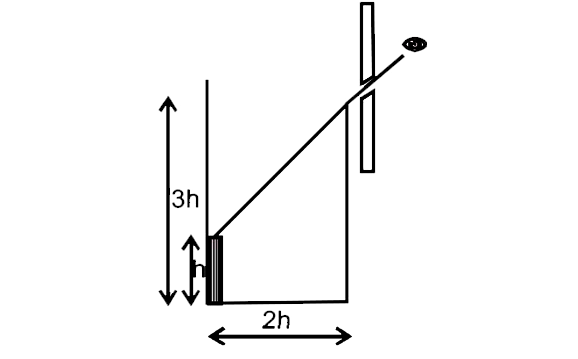 View Solution
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 View Solution
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
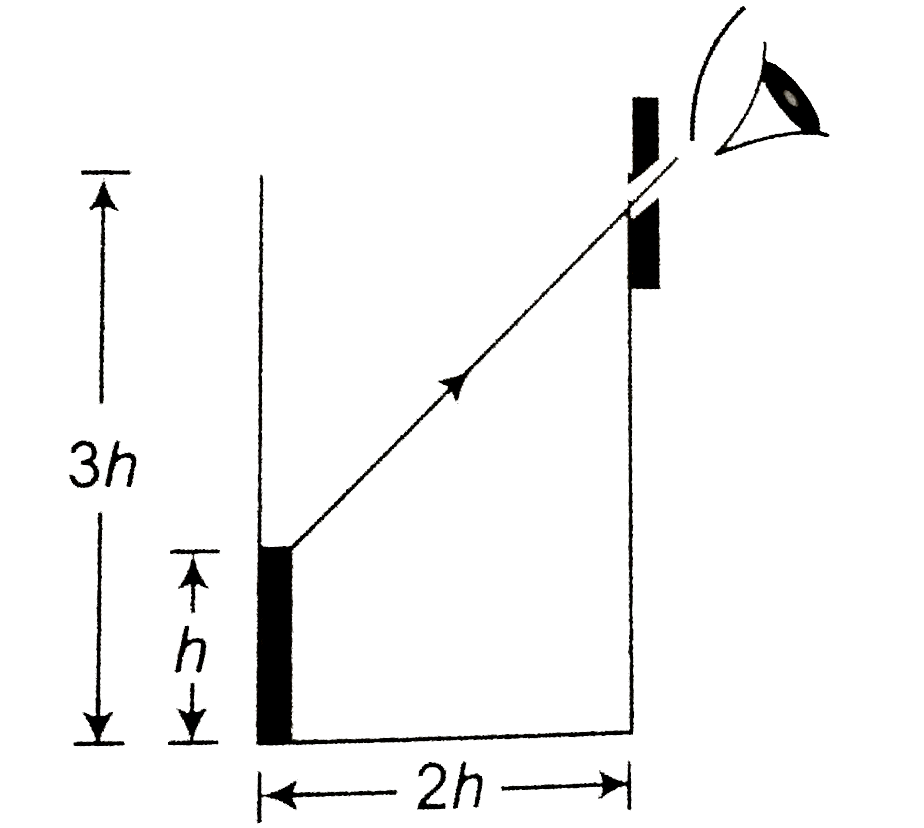 View Solution
View Solution

