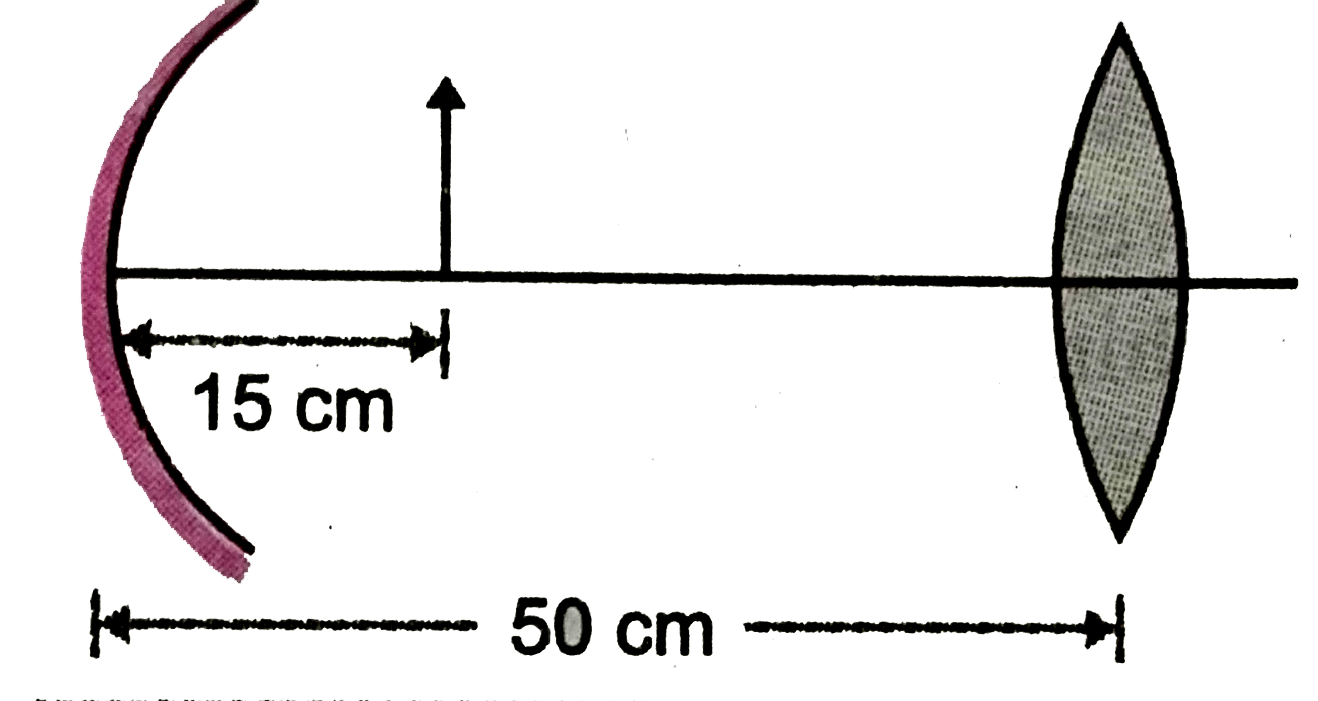
Consider a concave mirror and a convex lens (refractive index 1.5) of focal length $10 c m$ each separated by a distance of $50 c m$ in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of $15 c m$ from the mirror. Its erect image formed by this combination has magnification $M_{1}$ . When this set up is kept in a medium of refractive index $7 / 6$ , the magnification becomes $M_{2}$ . The magnitude $(\frac{M_{2}}{M_{1}})$ is :
$Consider a concave mirror and a convex lens (refractive index 1.5) of focal length 10 cm each separated by a distance of 50 cm in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification M1. When this set up is kept in a medium of refractive index 7//6, the magnification becomes M2. The magnitude ((M2)/(M1)) is : .$ .

Video Solution

Text Solution

Verified by Experts

Applying mirror formula
$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
$\frac{1}{v} = \frac{1}{f} - \frac{1}{u} = \frac{1}{- 10} + \frac{1}{15}$
$\frac{1}{v} = \frac{- 15 + 10}{150} = \frac{- 5}{150} = \frac{- 1}{30}$
$∵$ $v = - 30 c m$
For convex lens $u = | 2 f_{l} |$
Therefore image will have a magnification of l. when the set-up is kept in a medium The focal length of the lens will change
$\frac{\frac{1}{f_{l}}}{\frac{1}{f_{l}}}$ )))=(((n_l)/(n_s)-1))/(((n_l)/(n_s^( $)) - 1)) \Rightarrow (f_{l}$ ))/(10)=[[(1.5)/(1)-1]]/([1.5/((7)/(6))-1]) $< b r >$ impliesf_l^ $= 17.5 c m$
Applying lens formula $\frac{1}{v} - \frac{1}{u} = \frac{1}{f_{l}}$ ) $< b r >$ (1)/(v)-(1)/(-20)=(1)/(17.5)impliesv=15=40cm $< b r >$ M_l^= $M a g n if i c a t i o n b y \leq n s$ =(v)/(u)=(140)/(-20)=-7 $< b r > N o w$ [[M_2)/(M_1)]=|(MmirrorxxM_l^ $\frac{)}{M m i r r or \times M_{l}} ∣ = 7$

Updated on:21/07/2023