A student measures the focal length of a convex lens by putting an object pin at a distance u from the lens and measuring the distance v of the image pin. The graph between u and v plotted by the student should look like
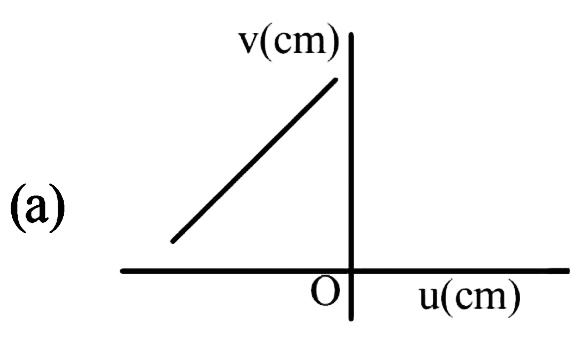
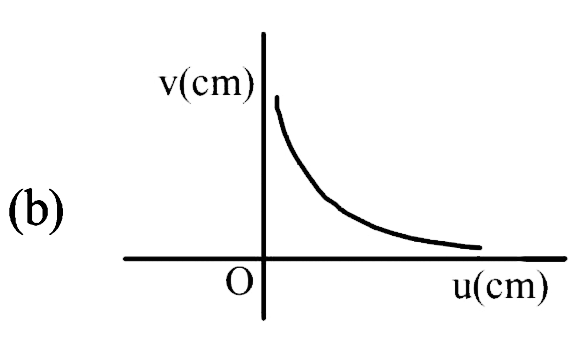
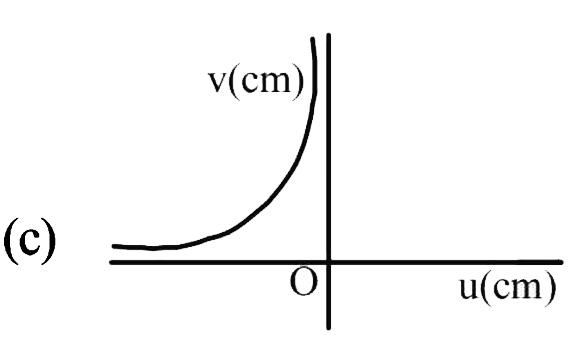
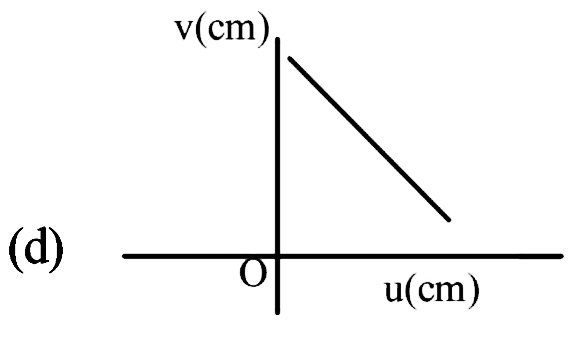
The correct Answer is:C
To solve the problem of how the graph between the object distance u and the image distance v for a convex lens looks, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula for a convex lens is given by:
1f=1v−1u
where:
- f is the focal length of the lens (positive for a convex lens),
- u is the object distance (negative in the Cartesian convention),
- v is the image distance (positive for real images).
Step 2: Rearranging the Lens Formula
We can rearrange the lens formula to express v in terms of u:
1v=1f+1u
Taking the reciprocal gives:
v=fuu+f
Step 3: Analyze the Relationship
From the rearranged formula, we can see that as u increases (moving the object further away from the lens), v will also increase. However, the relationship is not linear; it is hyperbolic because of the 1u term.
Step 4: Determine the Nature of the Graph
Since the relationship between u and v is of the form v=fuu+f, it indicates a hyperbolic relationship. The graph will curve towards the axes, specifically in the first quadrant where u is negative and v is positive.
Step 5: Identify the Correct Graph Option
Given the nature of the graph (hyperbolic), we can eliminate options that suggest a linear relationship. The correct graph should show a curve that approaches the axes but never touches them, confirming that as u approaches negative infinity, v approaches f.
Conclusion
The graph between u and v plotted by the student should look like a hyperbola in the first quadrant, confirming that the correct option is option C.
---
The lens formula for a convex lens is given by:
1f=1v−1u
where:
- f is the focal length of the lens (positive for a convex lens),
- u is the object distance (negative in the Cartesian convention),
- v is the image distance (positive for real images).
We can rearrange the lens formula to express v in terms of u:
1v=1f+1u
Taking the reciprocal gives:
v=fuu+f
From the rearranged formula, we can see that as u increases (moving the object further away from the lens), v will also increase. However, the relationship is not linear; it is hyperbolic because of the 1u term.
Since the relationship between u and v is of the form v=fuu+f, it indicates a hyperbolic relationship. The graph will curve towards the axes, specifically in the first quadrant where u is negative and v is positive.
Given the nature of the graph (hyperbolic), we can eliminate options that suggest a linear relationship. The correct graph should show a curve that approaches the axes but never touches them, confirming that as u approaches negative infinity, v approaches f.
The graph between u and v plotted by the student should look like a hyperbola in the first quadrant, confirming that the correct option is option C.
Topper's Solved these Questions
Similar Questions
Three students measured the focal length of a convex lens using parallel rays from distant object. All of the measured the distance between the lens and the inverted image on the screen. Student A saw a sharp image on the screen and labelled the distance as f1. Student B saw a slightly larger blurred image on the screen and labelled the distance as f2. Student C saw a slightly smaller blurred image on the screen and labelled the distance as f3 . What is the relation between the three measurements?
View SolutionThree students measured the focal length of a convex lens using parallel rays from distant object. All of the measured the distance between the lens and the inverted image on the screen. Student A saw a sharp image on the screen and labelled the distance as f1. Student B saw a slightly larger blurred image on the screen and labelled the distance as f2. Student C saw a slightly smaller blurred image on the screen and labelled the distance as f3 . What is the relation between the three measurements?
View Solution
Knowledge Check
An object is situated at a distance off/2from a convex lens of focal lengthfDistance of image will be-
A+(f/2)B+(f/3)C+(f/4)D−fThree students measured the focal length of a convex lens using parallel rays from a distant object. All of the measured the distance between the lens and the inverted image on the screen.
(i) Student A saw a sharp image on the screen and labelled the distance as f1
(ii) Student B saw a slightly larger blurred image on the screen and labelled the distance as f2
(iii) Student C saw slightly smaller blurred image on the screen and labelled the distance as f3
The relation between the three measurements would most likely be :Af1=f2=f3Bf1<f2<f3Cf3<f1<f2Df1<f2 and f1=f3To find the focal length of a convex lens, an image of a far located tree is obtained on a screen. For this the distance measured is:
AOnly of between screen and treeBOnly of between lens and screenCOnly of between lens and treeDBetween screen and tree and lens & screen
A small pin of size 5 mm is placed along principal axis of a convex lens of focal length 6cm at a distance 11cm from the lens. Find the size of image of pin.
[7.2 mm]
View SolutionThe graph between the image distance (v ) and object distance (u) from the convex lens is
View SolutionA convex lens forms a virtual image when an object is placed at a distance of 18cm from it. The focal length must be
View SolutionFor a convex lens, if real image is formed the graph between (u+v) and u or v is as follows
View SolutionA convex lens of focal length f produces a real image m times the size of an object, then the distance of the object from the lens is
View Solution
