Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
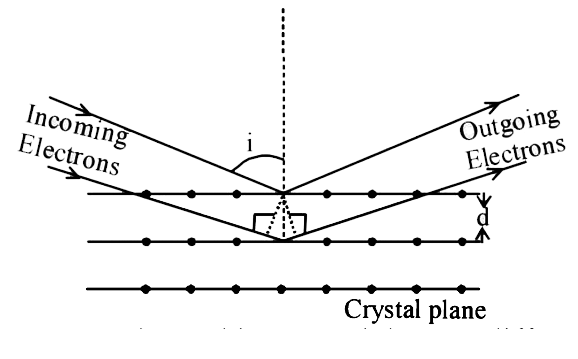
$Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely Electron accelerated by potential V are diffracted from a crystal if d = 1 Å and i = 30^(@), V should be about (h = 6.6 xx 10^(-34) Js, m(e) = 9.1 xx 10^(-31) kg , e = 1.6 xx 10^(-19)C)$
Electron accelerated by potential $V$ are diffracted from a crystal if $d = 1 Å and i = 30^{\circ}, V$ should be about $(h = 6.6 \times 10^{- 34} J s, m_{e} = 9.1 \times 10^{- 31} k g, e = 1.6 \times 10^{- 19} C)$

$2000 V$

$50 V$

$500 V$

$1000 V$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Using Bragg's equation $2 d sin θ = n λ$
$H r e r n = 1, θ = 90 - 1 = 90 - 30 = 60^{\circ}$
$2 d sin θ = l a n b d a$ …..(i)

Also $λ = \frac{12.27}{\sqrt{V}} \times 10^{- 10} m$ ……(ii)
$o m (i) and (i i)$ 2 xx 10^(-10) xx sin 60^(@)= (12.27)/(sqrt(V)) xx 10^(-10) $< b r >$ v = ((12.27)^(2))/(3) = 50 V

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Knowledge Check

Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely

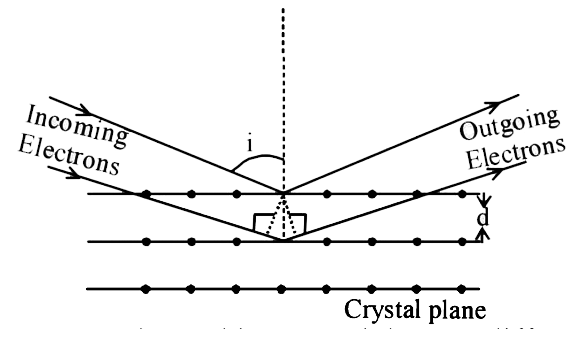
If a strong diffraction peak is observed when electrons are incident at an angle $i$ from the normal to the crystal planes with distance $d$ between them (see fig) de Brogle wavelength $λ_{d B}$ of electrons can be calculated by the relationship (n is an intenger)
A $d sin i = n λ_{d B}$
B $2 d cos i = n λ_{d B}$
C $2 d sin i = n λ_{d B}$
D $d cos i = n λ_{d B}$
Wave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure)

The surface of a metal is illuminated with the light of $400 n m$ . The kinetic energy of the ejected photoelectrons was found to be $1.68 e V$ . The work function of the metal is : ( $h c = 1240 e V - n m$ )
A $1.51 e V$
B $1.68 e V$
C $3.09 e V$
D $1.42 e V$
Wave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure)

In an experiment, electrons are made to pass through a narrow slit of width 'd' comparable to either de-Broglie wavelength. They are detected on a screen at a distance 'D' from the slit

The following graphs that can be expected to represent the number of electrons 'N' detected as a function of the detector position 'y' ( $y = 0$ corresponds to the middle of the slit) is
A
B
C
D