Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
4v/π
greater than 4v/π
less than 4v/π
zero
The correct Answer is:A
Figure shows the particles each moving with speed v but in different directions. Consider any two particles of their velocities.
The , velocity of B w.r.t , A, i.e,
VAB=VB−VA
(in case of a pair of particle A and particle B)
i.e,VBA=√v2+v2−2vvcosθ
⇒VBA=√2v2(1−cosθ)
=2vsin(θ2)
So, relative vleocity of overall pairs
vtrel=∫2π0vreldθ∫2π0dθ
=∫2π02vsin(θ/2)dθ∫2π0dθ
=2v×2[−cos.θ2]2π02π
∴ vrel=4vπ
Topper's Solved these Questions
Similar Questions
A particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View Solution
Knowledge Check
- Question 1 - Select One
Consider a collection of a large number of particles each with speed v in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
A>vB<vC=vDnone of these - Question 2 - Select One
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
AvB(π/4)vC(4/π)vDZero - Question 3 - Select One
Two bodies are moving in opposite direction with speed V. What is the magnitude of their relative velocity ?
A.0,BV,CY2D2V.
In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :
View SolutionIn a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is:
View SolutionA particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the avergae velocity for its motion form A to
View SolutionThe fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
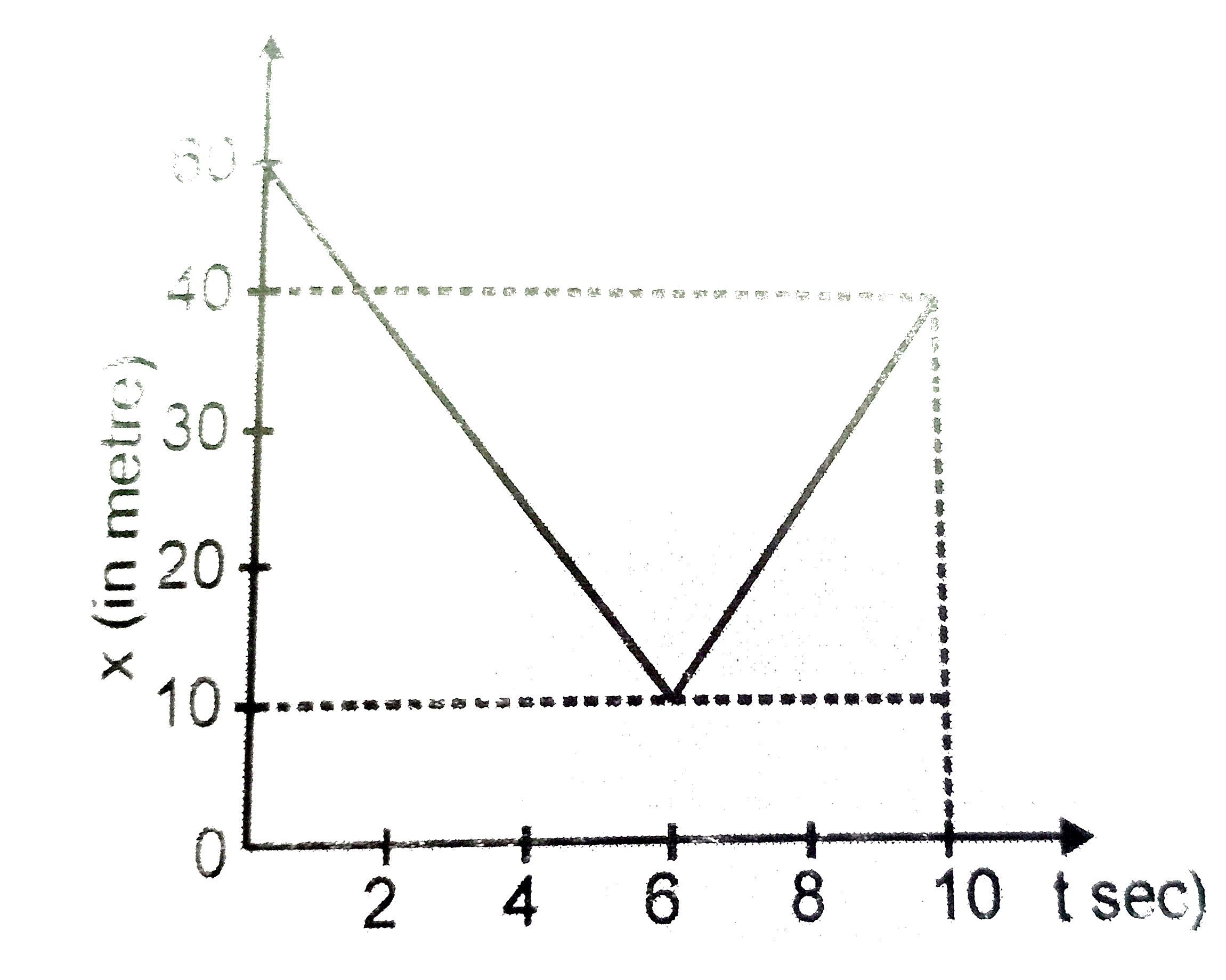 View Solution
View SolutionAssertion : Particle A is moving Eastwards and particle B Northwards with same speed. Then, velocity of A with respect to B is in South-East direction.
Reason : Relative velocity between them is zero as their speeds are same.View Solution

