The length of the common chord of the two circles x2+y2−4y=0 and x2+y2−8x−4y+11=0 is
A
√1454 cm
B
√112cm
C
√135 cm
D
√1354cm
Video Solution
Text Solution
The correct Answer is:D
Given , equation of cirlcesare
x2+y2−4y=0
and x2+y2−8x−4y+11=0
∴ Equation of chord is
x2+y2−4y−(x2+y2−8x−4y+11)=0
⇒ 8x11=0
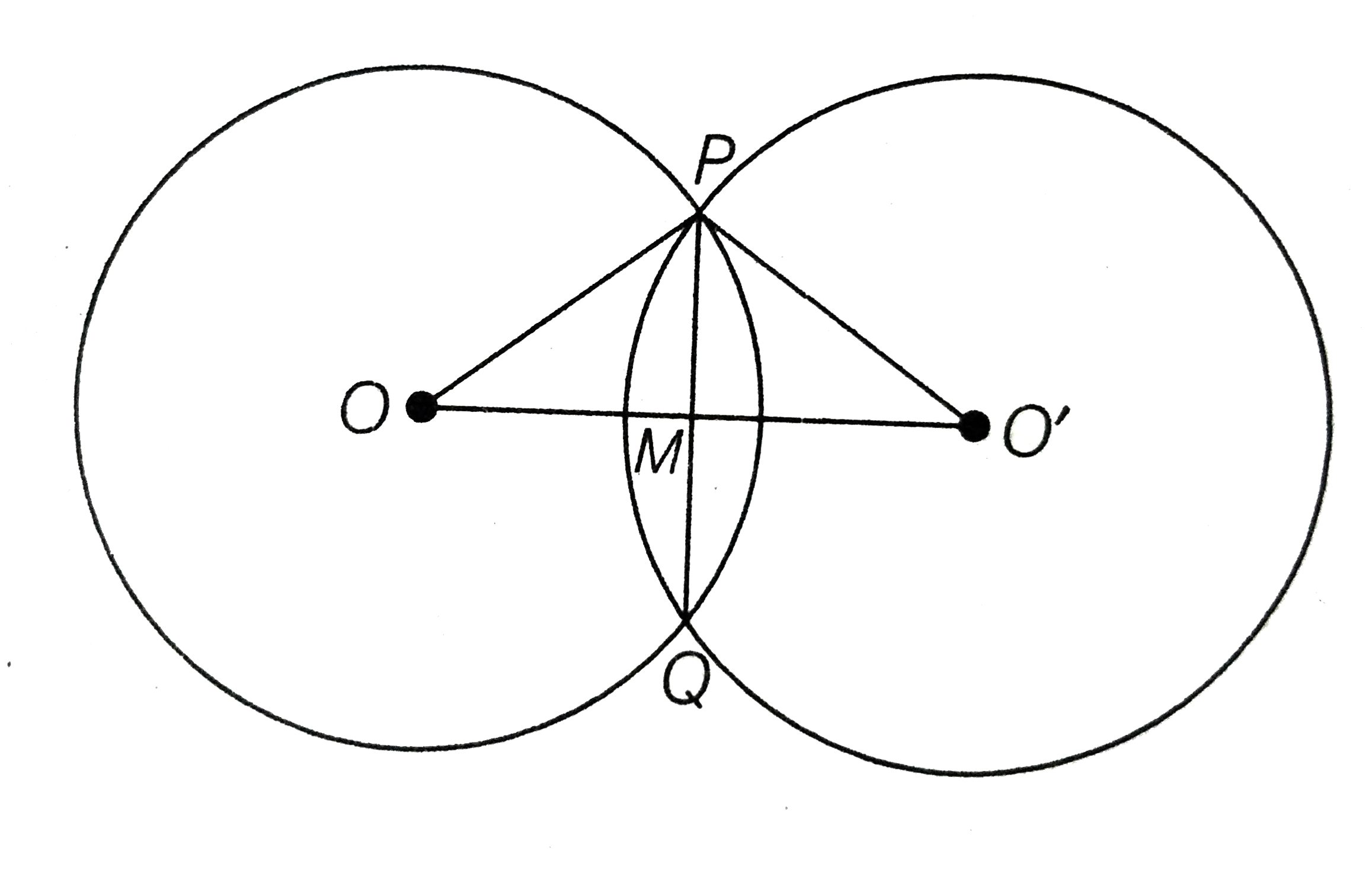
So , centre and radius of first circle are O(0,2) and OP = r= 2.
Now , perpendicular distance form O(0,2) to the line 8x - 11 is
d=OM=|8×0−11|√82=118
In ΔOMP,PM=√OP2−OM2
=√22−(118)2=√4−12164
=√256−12164=√1354cm
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The length of the common chord of the two circle x2+y2−4y=0 and x2+y2−8x−4y+11=0 is
A√1454 cmB√112 cmC√135 cmD√1354 cmThe length of the common chord of the circles x2+y2−2x−1=0 and x2+y2+4y−1=0, is
A√15/2B√15C2√15Dnone of theseThe length of the common chord of the circles x2+y2+2x+3y+1=0 and x2+y2+4x+3y+2=0 is
A92B2√2C3√2D32
The lenght of the common chord of circles x2+y2−6x−16=0andx2+y2−8y−9=0 is
View SolutionThe length of the common chord of the circles x2+y2−2x+4y−20=0,x2+y2+6x+10y−2=0 is
View SolutionThe two circles x2+y2−5=0 and x2+y2−2x−4y−15=0
View SolutionThe two circles x2+y2−5=0 and x2+y2−2x−4y−15=0
View SolutionWhich of the following is a point on the common chord of the circles x2+y2+2x−3y+6=0 and x2+y2+x−8y−13=0 ?
View Solution
