In SHM restoring force is F=−kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon
K,A and M
k,x, M
k,A
k,x
The correct Answer is:C
In SHM, the total energy =potential energy+kinetic energy
or E=U+K
=12mω2x2+12mω2(A2−x2)
=12mω2A2=12kA2
where k=force constant =mω2
Thus, total energy dependents on k and A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
There is a body having mass m and performinf SHM amplitude a There is a restroring force F=−Ks where x is the displacement The total energy of body depends upon
AK,xBK,aCK,a,xDK,a,vThe spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
A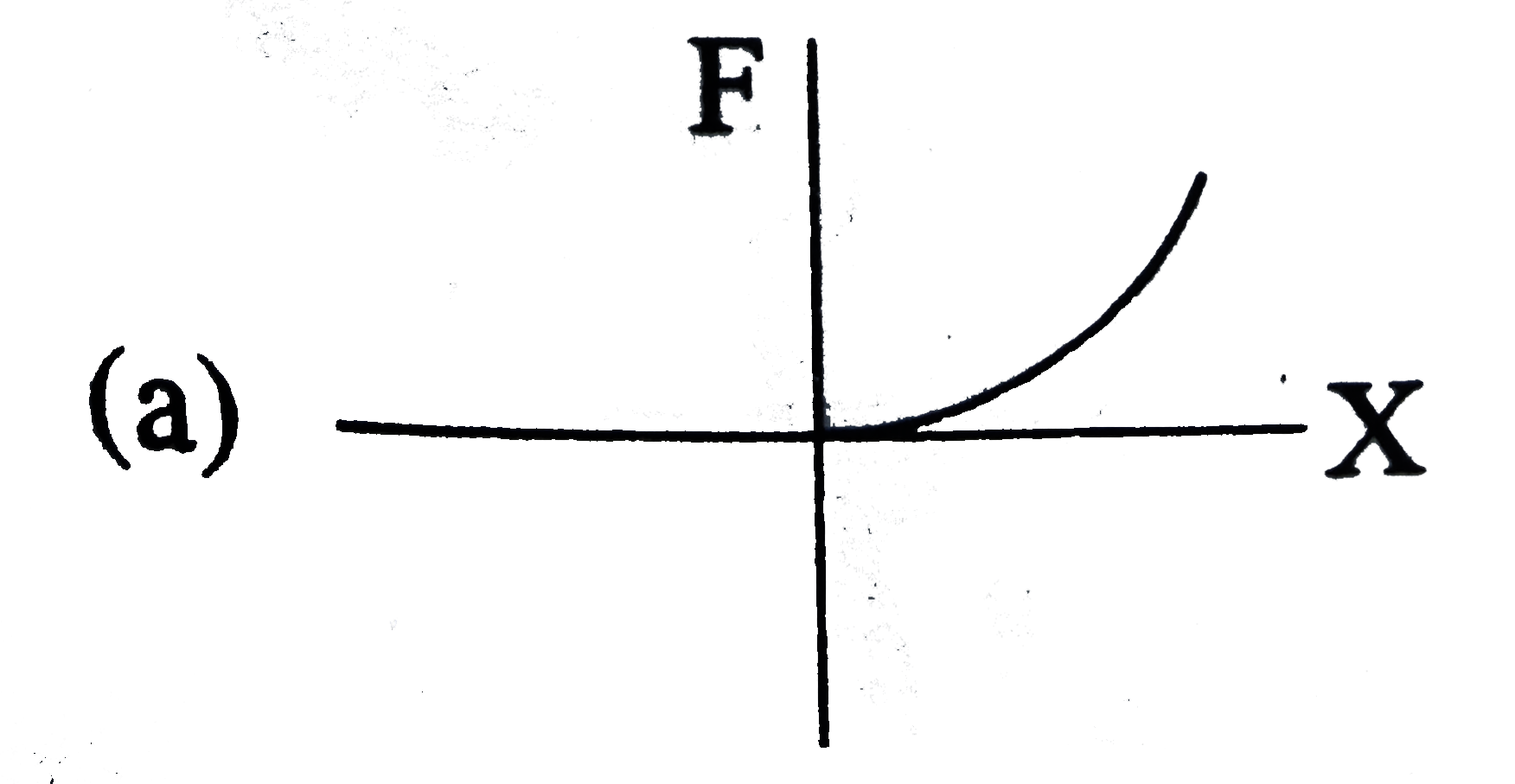 B
B C
C D
D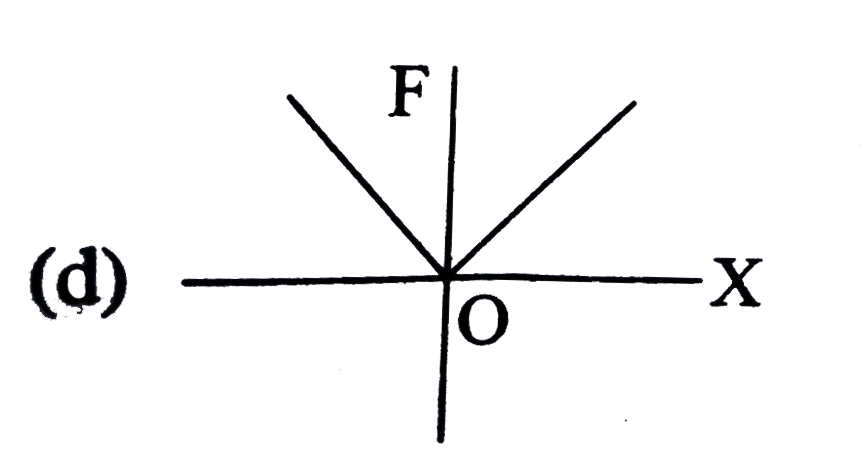
A particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
A12kx2B12kv2C12mv2D2mv2
The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionA quantity y is related to another quantity x by the equation y=kxa where k and a are constant. If percentage error in the measurement of x is p, then error is y depends upon
View SolutionThe restoring force F acting on a particle of mass (m) executing a S. H. M. is given by F= -Kx, where x is the displacement and K is a constant. Then the angular velocity of the particle is given by
View SolutionThe restoring force acting on a particle executing SHM is 10 N at a displacement of 2 cm from mean position. The restoring force at a displacement of 3 cm is
View SolutionConsider a spring that exerts the following restoring force :
F=−kx for x≥0
F=−4kx for x<0
A mass m on a frictionless surface is attached to the spring displaced to x=A by strectching the spring and released :
View Solution