A body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
g2√2
g2
3g2√2
g√2
The correct Answer is:C
To find the retardation of the block projected up along a rough inclined plane with an inclination of 45∘ and a coefficient of friction of 0.5, we can follow these steps:
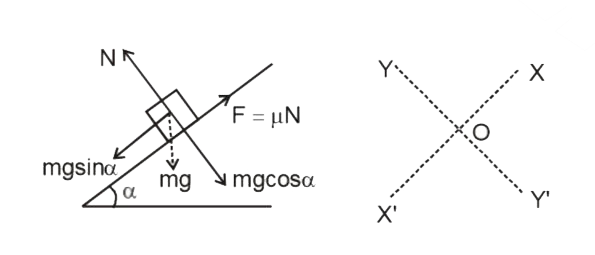
Step 1: Identify the Forces Acting on the Block
When the block is projected up the incline, two main forces act on it:
1. The gravitational force (mg) acting downwards.
2. The frictional force, which opposes the motion of the block.
Step 2: Resolve the Gravitational Force
The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
For θ=45∘:
- sin45∘=1√2
- cos45∘=1√2
Thus, the components become:
- mgsin45∘=mg⋅1√2
- mgcos45∘=mg⋅1√2
Step 3: Calculate the Normal Force
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ=mg⋅1√2
Step 4: Calculate the Frictional Force
The frictional force (f) can be calculated using the coefficient of friction (μ):
f=μN=μ(mgcosθ)=0.5⋅(mg⋅1√2)=0.5mg√2
Step 5: Determine the Net Force Acting on the Block
The net force (Fnet) acting on the block as it moves up the incline is given by:
Fnet=−mgsinθ−f
Substituting the values:
Fnet=−mg⋅1√2−0.5mg√2
Fnet=−mg⋅1+0.5√2=−mg⋅1.5√2
Step 6: Calculate the Retardation
Using Newton's second law, F=ma, we can find the retardation (a):
−mg⋅1.5√2=ma
Dividing both sides by m:
a=−g⋅1.5√2
Step 7: Substitute the Value of g
Using g≈9.8m/s2:
a=−9.8⋅1.5√2
Calculating this gives:
a≈−9.8⋅1.51.414≈−10.4m/s2
Thus, the retardation of the block is approximately 10.4m/s2.
Final Answer
The retardation of the block is 10.4m/s2.
---
When the block is projected up the incline, two main forces act on it:
1. The gravitational force (mg) acting downwards.
2. The frictional force, which opposes the motion of the block.
The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- sin45∘=1√2
- cos45∘=1√2
- mgsin45∘=mg⋅1√2
- mgcos45∘=mg⋅1√2
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ=mg⋅1√2
The frictional force (f) can be calculated using the coefficient of friction (μ):
f=μN=μ(mgcosθ)=0.5⋅(mg⋅1√2)=0.5mg√2
The net force (Fnet) acting on the block as it moves up the incline is given by:
Fnet=−mgsinθ−f
Substituting the values:
Fnet=−mg⋅1√2−0.5mg√2
Fnet=−mg⋅1+0.5√2=−mg⋅1.5√2
Using Newton's second law, F=ma, we can find the retardation (a):
−mg⋅1.5√2=ma
Dividing both sides by m:
a=−g⋅1.5√2
Using g≈9.8m/s2:
a=−9.8⋅1.5√2
Calculating this gives:
a≈−9.8⋅1.51.414≈−10.4m/s2
The retardation of the block is 10.4m/s2.
Topper's Solved these Questions
Similar Questions
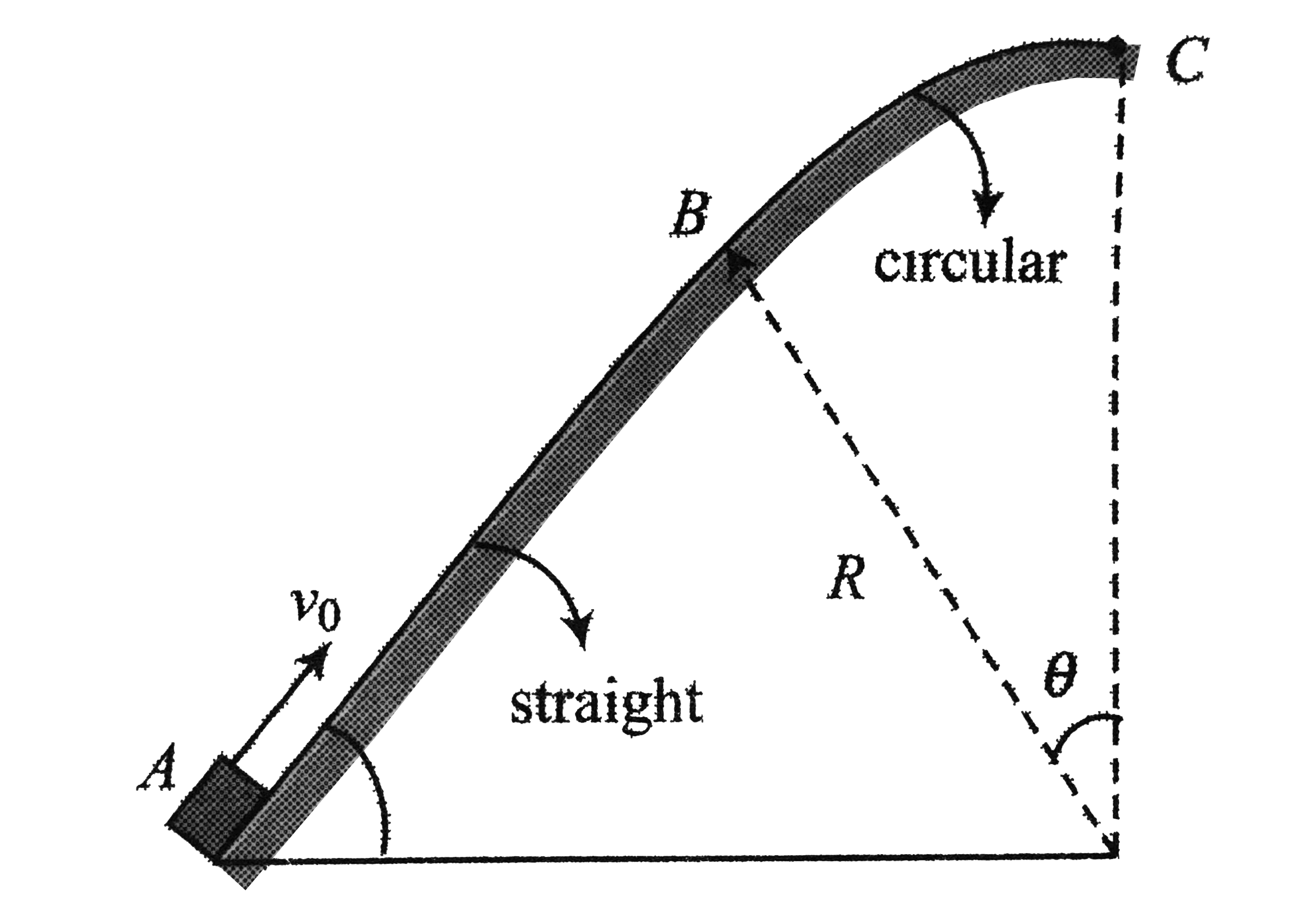
A block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View Solution
Knowledge Check
A block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
AThe time taken to slide down 9 m on the plane is 3 s.BThe velocity of block after moving 4 m is m/s.CThe block travels equal distances in equal intervals of time.DThe velocity of block increases linearly.For the equilibrium of a body on an inclined plane of inclination 45∘, the coefficient of static friction will be
Agreater than oneBless than oneCzeroDless than zeroA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
A−1√2JB1JC−√2JD−1J
A body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
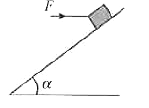
View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
View SolutionA body weighing 20 kg just slides down a rough inclined plane that rises 5 in 12. The coefficient of friction is
View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View SolutionA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View Solution