A mass is suspended from a spring have spring constant k is displaced veritcally and relased it oscillates with period T the weight of the mass suspended is (g= gravitatioanal acceleration)
kTg4π2
kT2g4π2
kTg2π2
kT2g2π2
The correct Answer is:c
Time period of oscillation of the block
T=2π√mk→T24π2=mk
or m2k4π2 n ltbgt weight of the mass w = mg =kT2g(4π)2

Topper's Solved these Questions
- MHTCET 2015BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MHTCET 2015EXERCISE - Chemistry
1 Videos
- MHTCET 2014BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MHTCET 2014EXERCISE - Physics
45 Videos
- MHTCET 2016BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MHTCET 2016EXERCISE - Physics
50 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View Solution
Knowledge Check
A flat spiral spring of force constant K is loaded with mass M and oscillates vertically with a time period T. Then the mass suspended to the free end is
A4π2KT2BKT24π2CKT4π2DKT4πA flat spiral spring of force constant k is loaded with mass M and oscillate about vertical with a time period T. Then the mass suspended to the free end is
A4π2kT2BkT24π2CkT4π2DkT4πA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
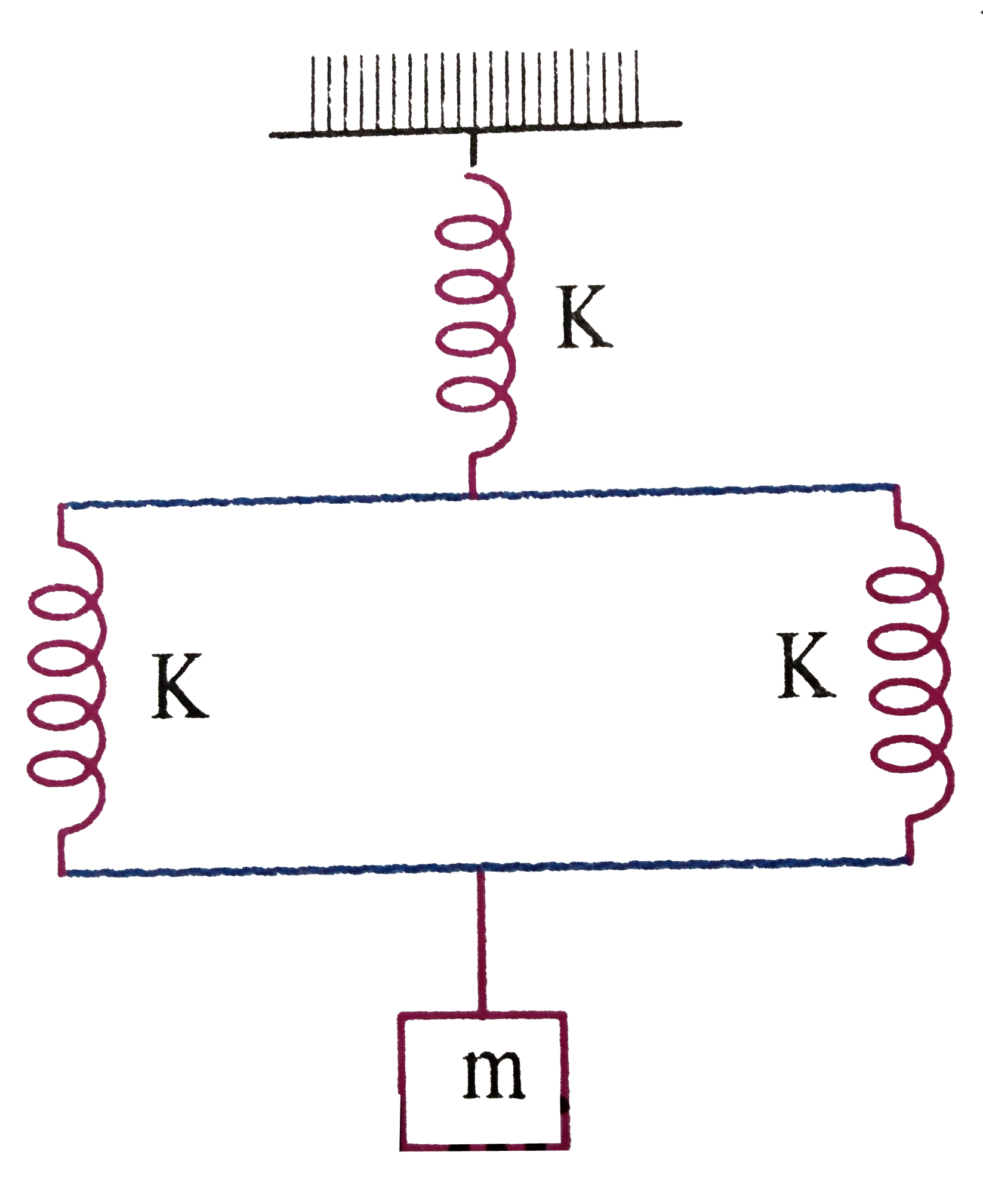 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
Periodic time of oscillation T1 is obtained when a mass is suspended from a spring and if another spring is used with same mass then periodic time of oscillation is T2 . Now if this mass is suspended from series combination of above springs then calculated the time period.
View SolutionPeriodic time of oscillation T1 is obtained when a mass is suspended from a spring if another spring is used with same mass then periodic time of oscillation is T2. Now if this mass is suspended from series combination of above spring then calculate the time period.
View SolutionWhen a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
View SolutionA mass of 4 kg suspended from a spring of spring constant 800Nm−1 executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum acceleration (in ms−2) of the mass is
View SolutionA mass of 1 kg is suspended from a spring. Its time period of oscillation on the earth is T. What will be its time periods at the centre of the earth?
View Solution
