A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
MRω4t
MRω2t
MRωt
MRωt
The correct Answer is:B
Given, mass of disc = M
Radius of disc =R
We know that, τ=lα . . . (i)
But τ=F×R
∴ l=MR22
and α=ωt
Therefore, F×R=MR22×ωt
F=MR2×ωt F=MRω2t
Topper's Solved these Questions
Similar Questions
A flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of 2rad s−2 ?
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View Solution
Knowledge Check
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
AMRω4tBMRω2tCMRωtDMRωtA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
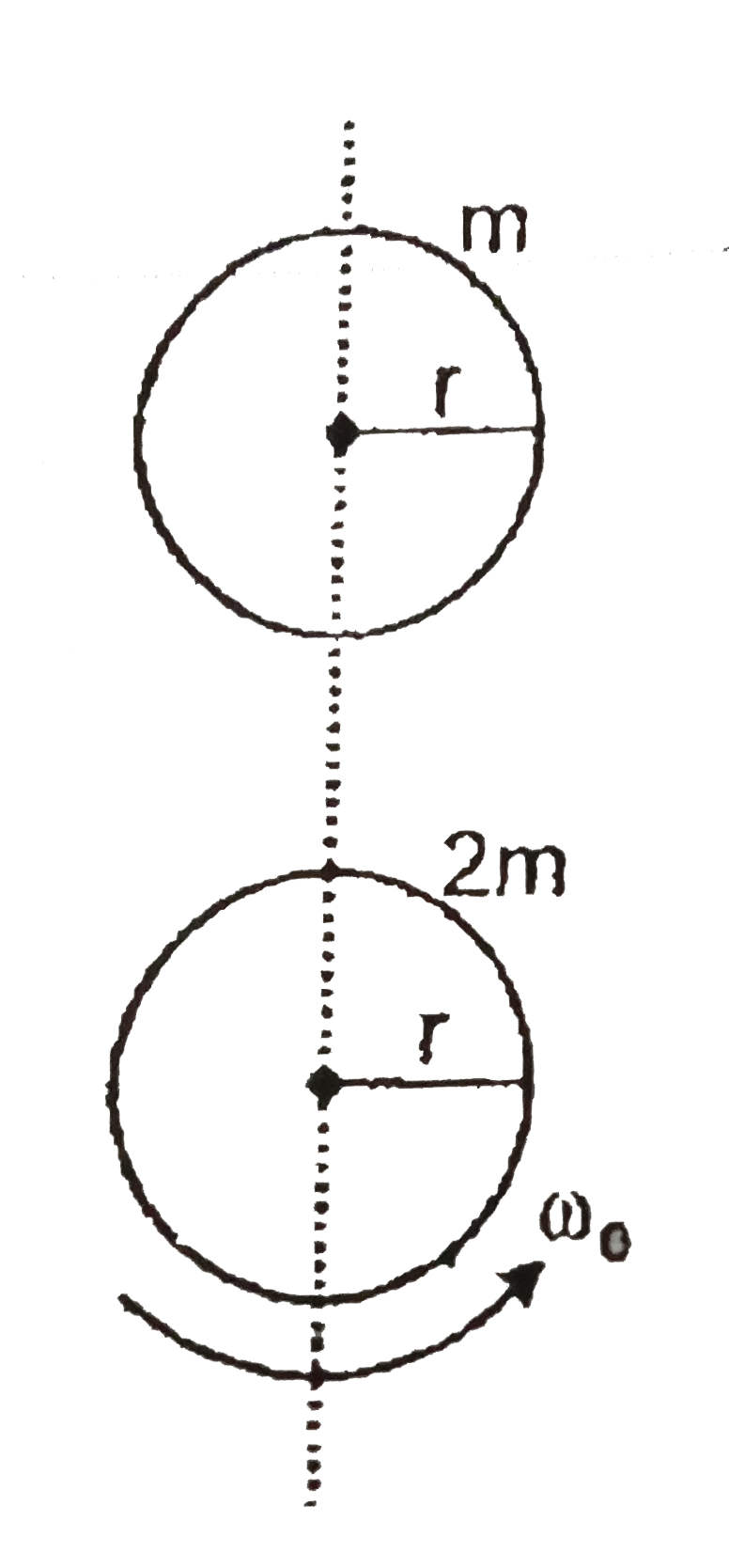
Angular velocity 'ω' when both discs start rotating together without slippingA2ω03B3ω04Cω03Dω02A disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
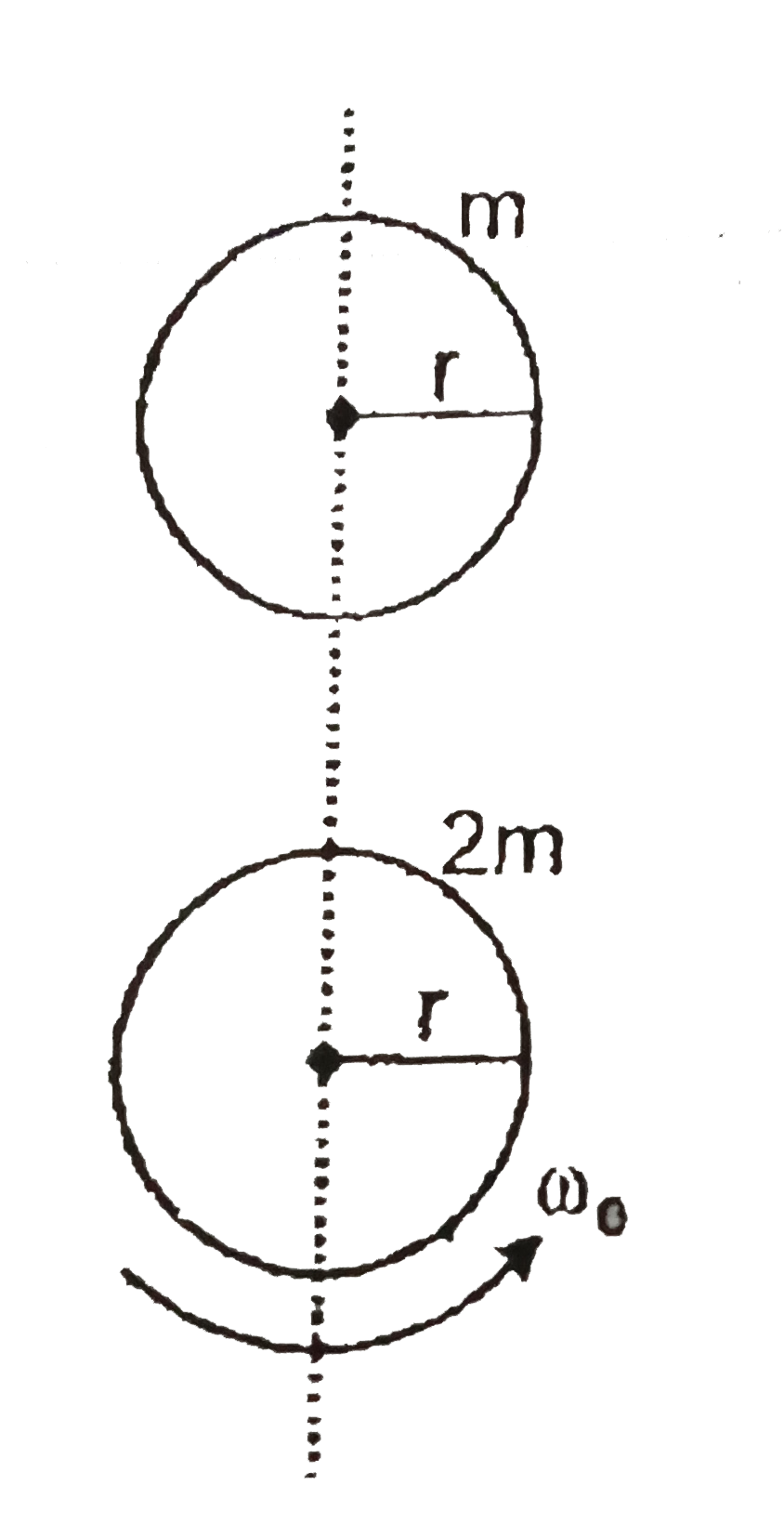
Time elapsed in this processAω0RμgB2ω0RμgCω0R2μgDω0R4μg
A disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.

Loss in kinetic energy of system
View SolutionIf a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
View SolutionA uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity ω. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View Solution
