Question

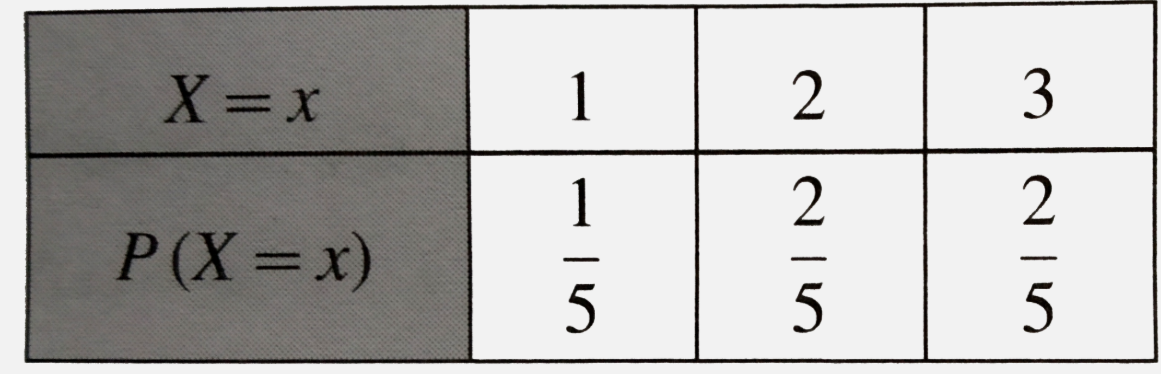
The probability mass function (p. m. f.) of X is given below :
$\left|\begin{array}{cccc}X=x& 1& 2& 3\\ P(X=x)& \frac{1}{5}& \frac{2}{5}& \frac{2}{5}\end{array}\right|$ find $E\left(X^2\right)$

Explanation

To find $$E\left(X^2\right)$$ using the given probability mass function (p.m.f.) of $$X$$, we will follow these steps:

Step 1: Identify the values of \( X \) and their corresponding probabilities
From the problem, we have:
- \( X = 1 \) with \( P(X=1) = \frac{1}{5} \)
- \( X = 2 \) with \( P(X=2) = \frac{2}{5} \)
- \( X = 3 \) with \( P(X=3) = \frac{2}{5} \)

Step 2: Write the formula for \( E(X^2) \)
The expected value \( E(X^2) \) is calculated using the formula:
\( E(X^2) = \sum (x^2 \cdot P(X=x)) \)
where the summation is over all possible values of \( X \).

Step 3: Substitute the values into the formula
Now we will substitute the values of \( X \) and their probabilities into the formula:
\( E(X^2) = (1^2 \cdot P(X=1)) + (2^2 \cdot P(X=2)) + (3^2 \cdot P(X=3)) \)

Substituting the values:
\( E(X^2) = (1^2 \cdot \frac{1}{5}) + (2^2 \cdot \frac{2}{5}) + (3^2 \cdot \frac{2}{5}) \)

Calculating each term:
- For \( X=1 \): \( 1^2 \cdot \frac{1}{5} = 1 \cdot \frac{1}{5} = \frac{1}{5} \)
- For \( X=2 \): \( 2^2 \cdot \frac{2}{5} = 4 \cdot \frac{2}{5} = \frac{8}{5} \)
- For \( X=3 \): \( 3^2 \cdot \frac{2}{5} = 9 \cdot \frac{2}{5} = \frac{18}{5} \)

Step 4: Sum the results
Now we sum these results:
\( E(X^2) = \frac{1}{5} + \frac{8}{5} + \frac{18}{5} \)
Combining the fractions:
\( E(X^2) = \frac{1 + 8 + 18}{5} = \frac{27}{5} \)

Final Answer
Thus, the expected value \( E(X^2) \) is:
\( \boxed{\frac{27}{5}} \)