Examine whether the following logical statement pattern is tautology, contradication or contingency.
$[(p \to q) \land q] \to p$

Video Solution

Text Solution

Verified by Experts

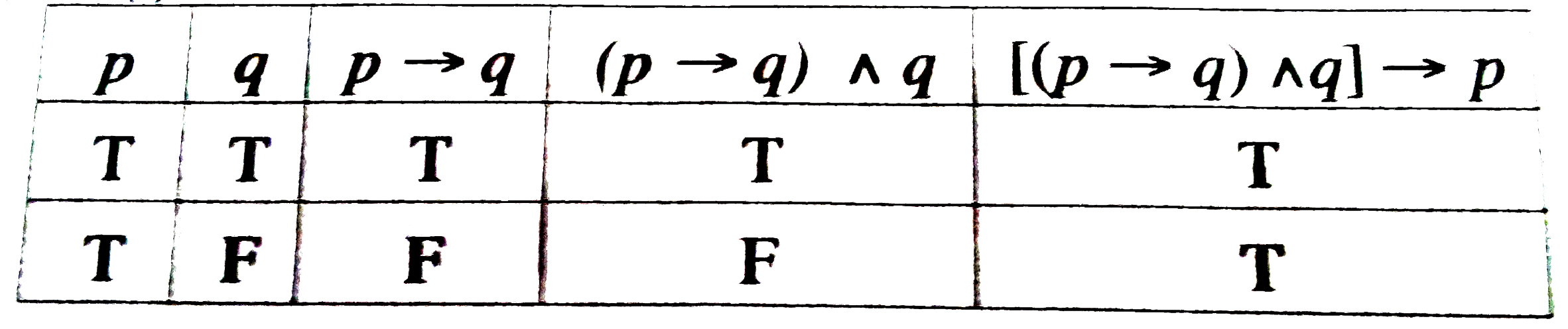
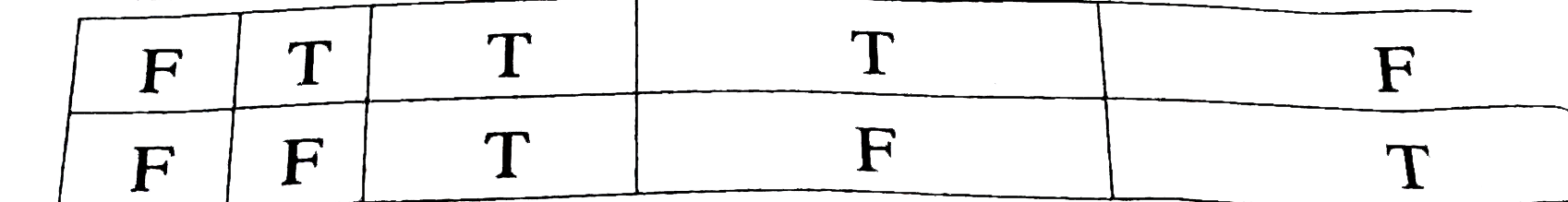
Since the truth table contains neither all T nor all F in the last column,.
$∴ p [(p \to q) \land q] \to p$ is a continency.

Updated on:21/07/2023

|

Class 12 MATHS MARCH 2016

Topper's Solved these Questions

MARCH 2016BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2016EXERCISE - SECTION II
20 Videos
MARCH 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2015EXERCISE - SECTION-II
20 Videos
MARCH 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2017EXERCISE - SECTION-II
20 Videos

Similar Questions

Knowledge Check

Which of the following statement pattern is a tautology?
A $p \lor (q \to p)$
B $~ q \to ~ p$
C $(q \to p) \lor (~ p \to q)$
D $p \land ~ p$
Which of the following statement pattern is a tautology?
A $p \lor (q \to p)$
B $~ q \to ~ p$
C $(q \to p) \lor (~ p \leftrightarrow q)$
D $p \land ~ p$
The inverse of logical statement $p \to q$ is
A $~ p \to ~ q$
B $p \leftrightarrow q$
C $q \to p$
D $q \leftrightarrow p$

GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS- MARCH 2016-SECTION II

Home
Ask Doubt
Profile