Solve the following LPP by using graphical method.
Maximize :
Subject to Also find maximum value of Z.
Video Solution
Text Solution
Maximum :
Subject to and .
Now,
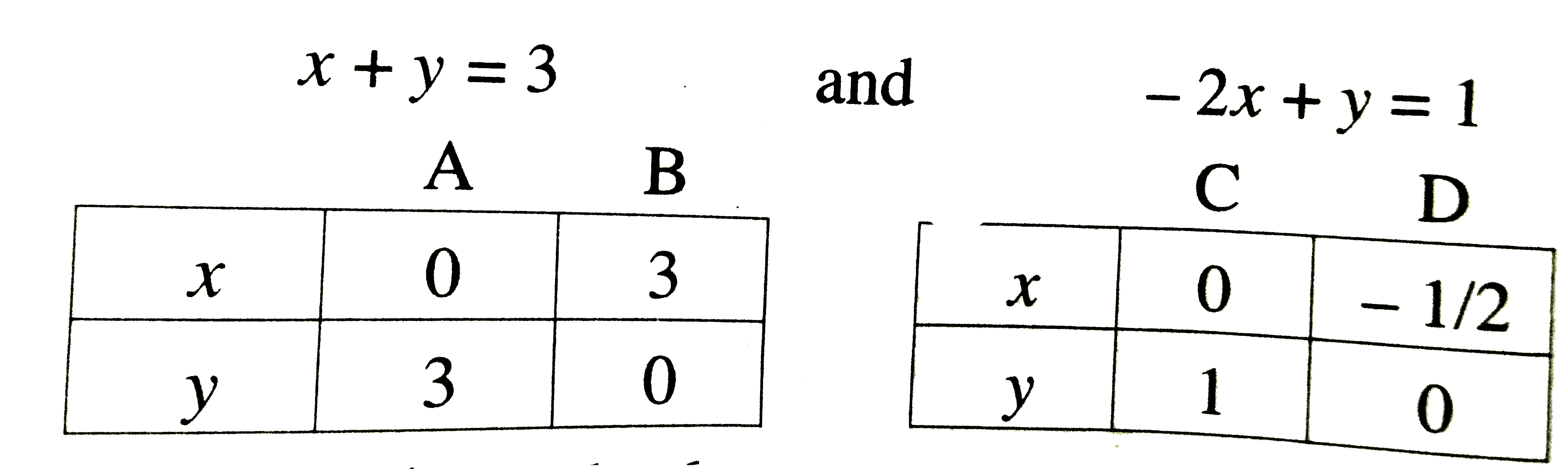
First we draw the lines AB, CD and RS whose equations are and respectively.
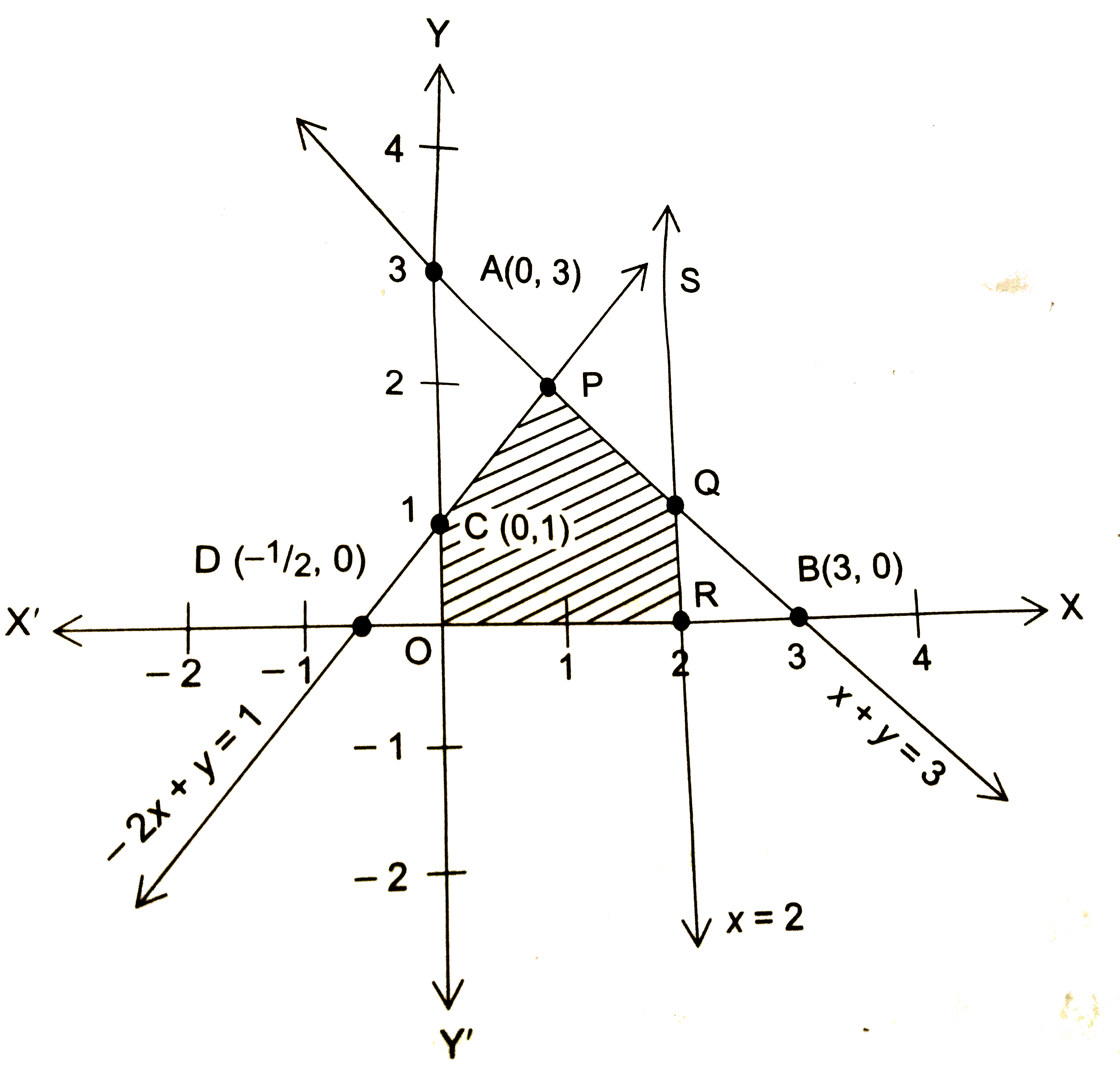
The feasible region is ORQPCO which is shaded in the figure. The vertices of the feasible region are O and .
P is the point of intersection of the lines
and
Solving these equations we get point .
Q is the point of intersection of the lines and x = 2
Putting x = 2 in we get y = 1
Point Q(2,1) Putting x = 2 in , we get y = 1
Point Q (2, 1)
The value of the objective function at these vertices are

The maximum value of z is 16, when x = 2 and y = 1.
|
Topper's Solved these Questions
- OCTOBER 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2014EXERCISE - SECTION - II
19 Videos
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-D
13 Videos
- OCTOBER 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2015EXERCISE - SECTION -II
20 Videos
Similar Questions
Knowledge Check
If Z=2x + y subject to x≤4,y≤6,x+y≥6,x≥0,y≥0, then the maximum value of Z is
A18B10C6D14
y−2x≤1,x+y≤2,x≥0,y≥0
View Solution2x+y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.
View SolutionZ=4x+7y
x+2y≤20,x+y≤15,x≥0,y≥0.
View SolutionMaximize z=10x+25y, subject to x≤3,y≤3,x+y≤5,x≥0,y≥0.
View Solutionx+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View SolutionMaximize z=6x+4y, subject to
2x+3y≤30,3x+2y≤24,x+y≥3,x≥0,y≥0.
View SolutionZ=4x+y
x+y≤50,3x+y≤90,x≥0,y≥0
View Solution
