Define linear S.H.M. Show that S.H.M. Is a projection of U.C.M. on any diameter.
A metal sphere cools at the rate of $4^{\circ}$ C/min. when its temperature is $50^{\circ} C$ .Find its rate of cooling at $45^{\circ} C$ if the temperature of surroundings is $25^{\circ} C$ .

Text Solution

Verified by Experts

Linear S.H.M. Is the simplest kind of oscillatory motion in which a body when displced from its mean position, oscillates 'to and fro' about mean position and the restoring force (or acceleration) is always directed towards its mean position and its magnitude is directly towards its mean position and its magnitude is directly proportional to the displacement form the mean position.
Consider a particle P moving along the circumference of a circle of radius a with uniform angular speed of $ω$ in anticlockwise direction as shown.
Particles P along circumference of the circle has its projection particle on diameter AB at point M.

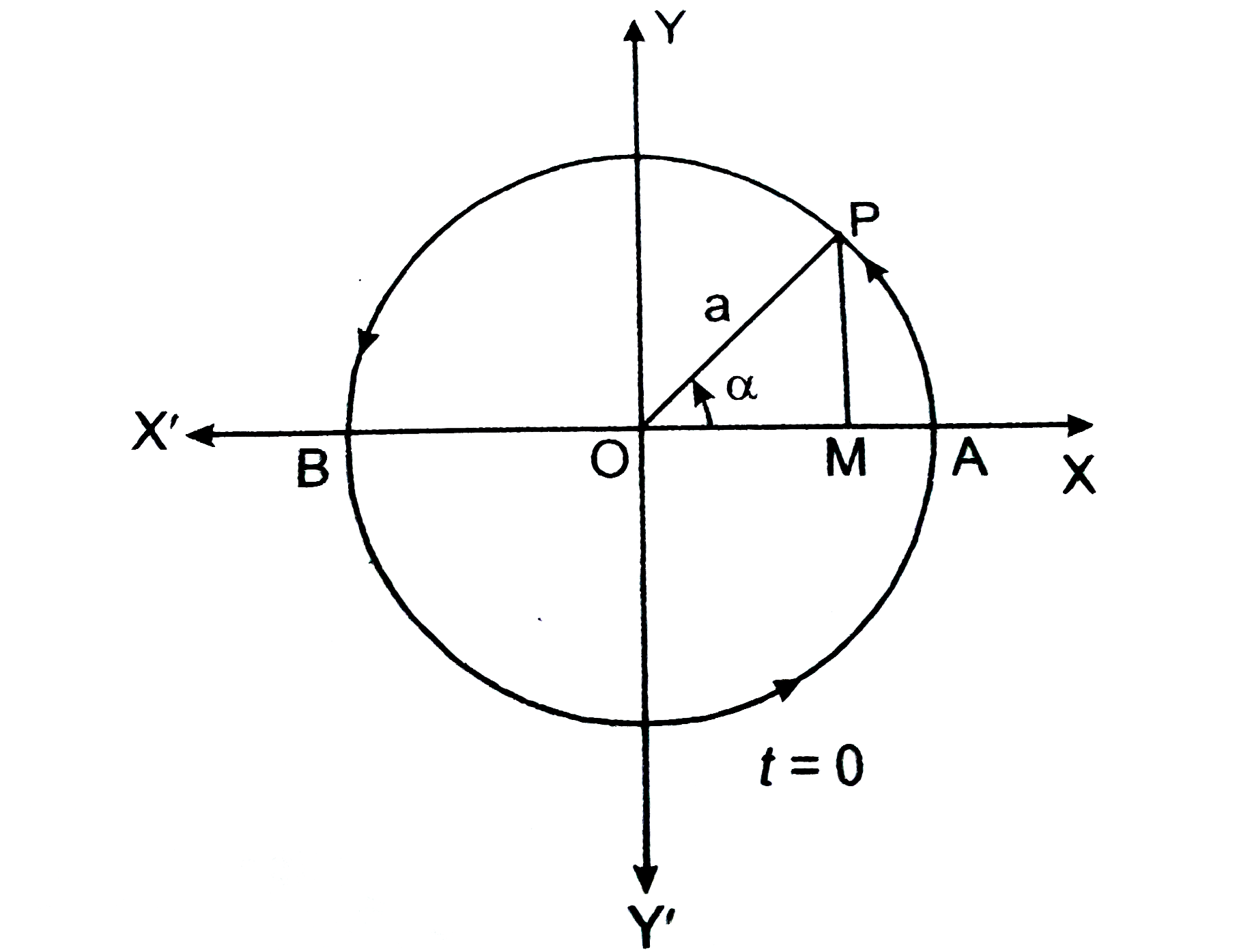
Suppose that particle P starts from the initial position with initial phase angle $α$ (angle between radius OP and the X- axis at the time $t = 0$ )
In time t, the angle between OP and X-axis is $(ω t + α)$ particle P moving with constant angular velocity $(ω)$ as shown.

$cos (ω t + α) - \frac{x}{a}$
$∴ x = a cos (ω t + α) ... (i)$
This is the expansion for displacement of particle M at time t.
As velocity of the particle is the time rate of change of displacement then we have
$v = \frac{d x}{d t} = \frac{d}{d t}$ $[a cos (ω t + α)]$
$∴ v = - a ω sin (ω t + α) ... (i i)$
As acceleration of particle is the time rate of change of velocity, we have
$a = \frac{d v}{d t} = \frac{d}{d t} [- a ω sin (ω t + α)]$
$∴ a = - a ω^{2} cos (ω t + α)$
$∴ a = - ω^{2} x$
Hence, the projection of a uniform circular motion on a diameter of a circle is simple harmonic motion.
Numerical :
Given that for the metal sphere,
${(\frac{d t h η}{d t})}_{1} = 4^{\circ} C / min$ .
$θ_{1} = 50^{\circ} C, θ_{2} = 45^{\circ} C$ and $θ_{0} = 25^{\circ} C$ .
By Newton's law of cooling,
$(\frac{d θ}{d t}) = k (θ - θ_{0})$
$∴ \frac{{(d θ / d t)}_{1}}{{(d θ / d t)}_{2}} = \frac{(θ_{1} - θ_{0})}{θ_{2} - θ_{1}})$
$∴ \frac{{(d θ / d t)}_{1}}{{(d θ / d t)}_{2}} = \frac{(50^{\circ} - 25^{\circ})}{(45^{\circ} - 25^{\circ})}$
$∴ {(\frac{d θ}{d t})}_{2} = \frac{20^{\circ}}{25^{\circ}} \times {(\frac{d θ}{d t})}_{1} = \frac{20^{\circ}}{25^{\circ}} \times 4 = 3.2$
$∴ {(\frac{d θ}{d t})}_{2} = {3.2}^{\circ} C / min$

Updated on:21/07/2023

Projection of U.C.M. along its any diameter is
Alinear S.H.M.
Bangular S.H.M.
Cneither linear S.H.M. nor angular S.H.M.
Dcomplex oscillatory motion
A body cools at the rate of $3^{\circ} C /$ min when its temperature is $50^{\circ} C$ . If the temperature of surroundings is $25^{\circ} C$ then the rate of cooling of the body at $40^{\circ} C$ is
A $2^{\circ} C$ /min
B ${2.4}^{\circ} C$ /min
C ${2.8}^{\circ} C$ /min
D ${1.8}^{\circ} C$ /min
A body cools at the rate of ${0.75}^{\circ} C / s$ when it is $50^{\circ} C$ above the surrounding. Its rate of cooling when it is $30^{\circ} C$ above the same surrounding is
A ${0.32}^{\circ} C / s$
B ${0.36}^{\circ} C / s$
C ${0.40}^{\circ} C / s$
D ${0.45}^{\circ} C / s$