Question

What are forced vibrations and resonance ? Show that only odd harmonics are present in an air column vibrating in a pipe closed at one end. A stretched wire emits a fundamental note of frequency 256 Hz. Keeping the stretching force constant and reducing length of the wire by 10cm, the frequency becomes 320 Hz. Calculate the original length of wire.

Explanation

Forced vibrations. The vibrations of body under action of external perodic force other than its naturral frequencfy are called forced vivrations.
Resonance : Resonance is a special case of forced vibrations. If an object is being forced to bibrate at its natural frequence, resonance will occur adn large amplitude vibrations can be observed. The resonant frequency is `f_(0)`.
Modes of vibration of air column in a pipe closed at one end :

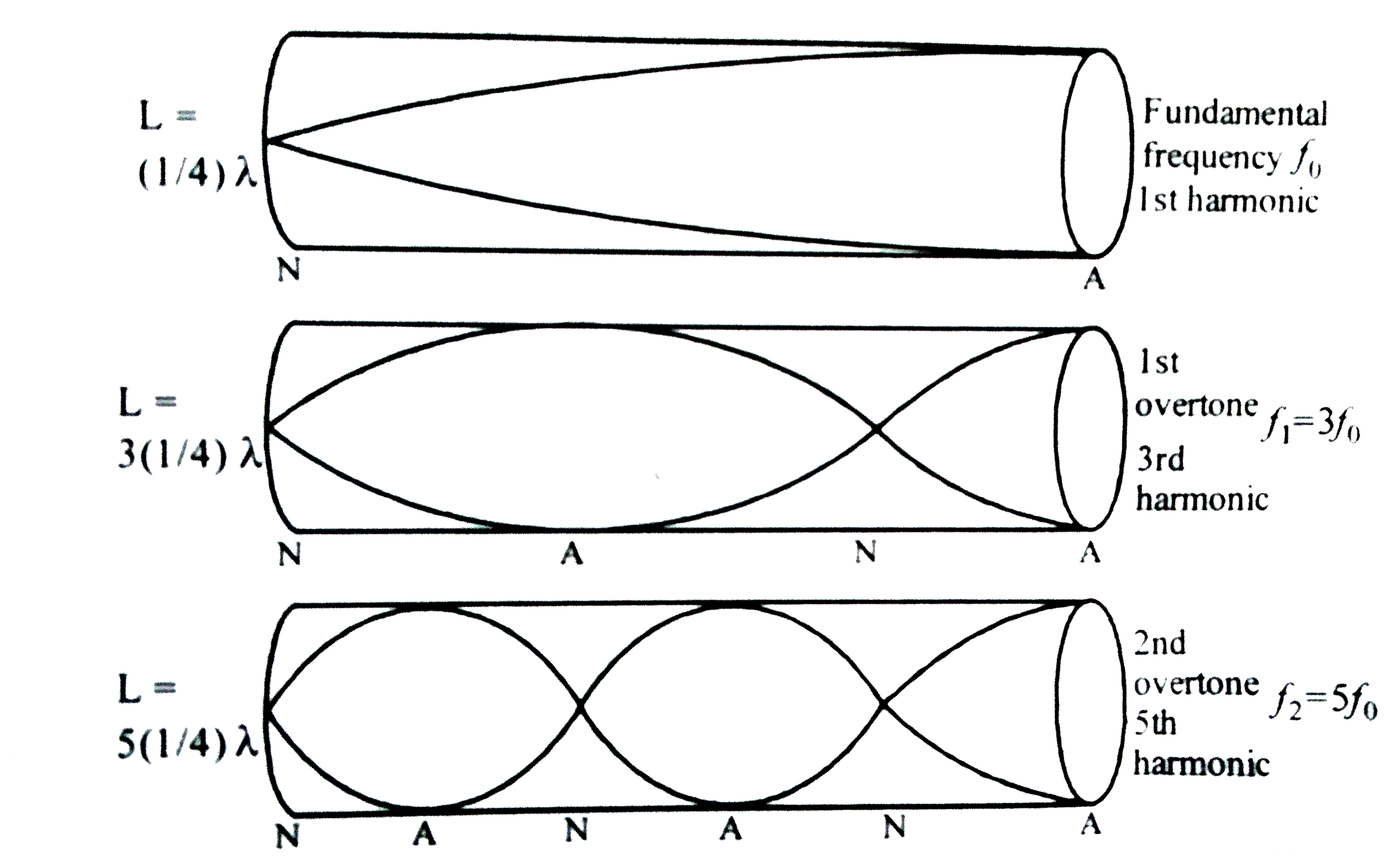
Thus, it can be seen that only odd harmonics are presetn as overtone in a mode of vibration of air column closed at onel end.
Numerical : The fundamental frequency of vibration ( the simplest mode with one vibrating segment ) is given by the relation.
`f=1/(2L)*sqrt(T/mu)`
where f is the frequency in Hz, T is the tension in the string in newton, `mu` is the mass per unit length of the string ( linear density ) in kg/m, and L is the length of the string in meters. Now, here `f_(1)=256 Hz, Deltal=10 cm = 0.1 m, f_(2)=320 Hz`.
The linear density remains the same as there is no change in the meterial of the wirel, also, the tension remains constant.
For first condition, `256=1/(2L)*sqrt(T/mu)`
`"or "L=1/(2(256))*sqrt(T/mu)`
`=1/(512)*sqrt(T/mu)" ...(i)"`
For second condition,
`320 = 1/(2(L - 0.1))*sqrt(T/mu)`
`"or "L-0.1=(1/(2320))*sqrt(T/mu)" ...(ii)"`
`"or "1/(512)*sqrt(T/mu)-0.1=1/640*sqrt(T/mu)`
` " or "sqrt(T/mu)[1/512-1/640]=0.1`
`sqrt(T/mu)[0*00039=0*1`
`" or "sqrt(T/mu)=256`
`"Thus, "L=1/(512)(256)m" "["using equation (i)"]`
`=0.5m = 50 cm`