Write molecularity of the following reaction :
2NO(s)+O2(g)→2NO2(g)
What is 'calcination' ? How does it differ from 'roasting' ?
Write resonating structures of ozone,
The decomposition of N2O5(g) at 320 K according to the following equation follows first order reaction :
N2O5(g)→2NO2(g)+12O2(g)
The initial concentration of N2O5(g) is 1⋅24×10−2mol.L−1 and after 60 minutes, 0⋅20×10−2mol.L−1. Calculate the rate constant of the reaction at 320 K.
Molecularity is the sum of the different reactants which take part in a chemical reaction. Thus, molecularity of the reaction.
2NO(g)+O2(g)→2NO2(g) is (2+1)=3
Calcination : Calcination is a process in which the ore of a metal or other solid material is heated to a high temperature below the melting point of the metal in absence of air or limited supply of air
Example : Decomposition of carbonate minerals as in the calcination of limestone to drive of CO2.
CaCO3(s)→CaO(s)+CO2(g)

The resonating structures of ozone are given below :
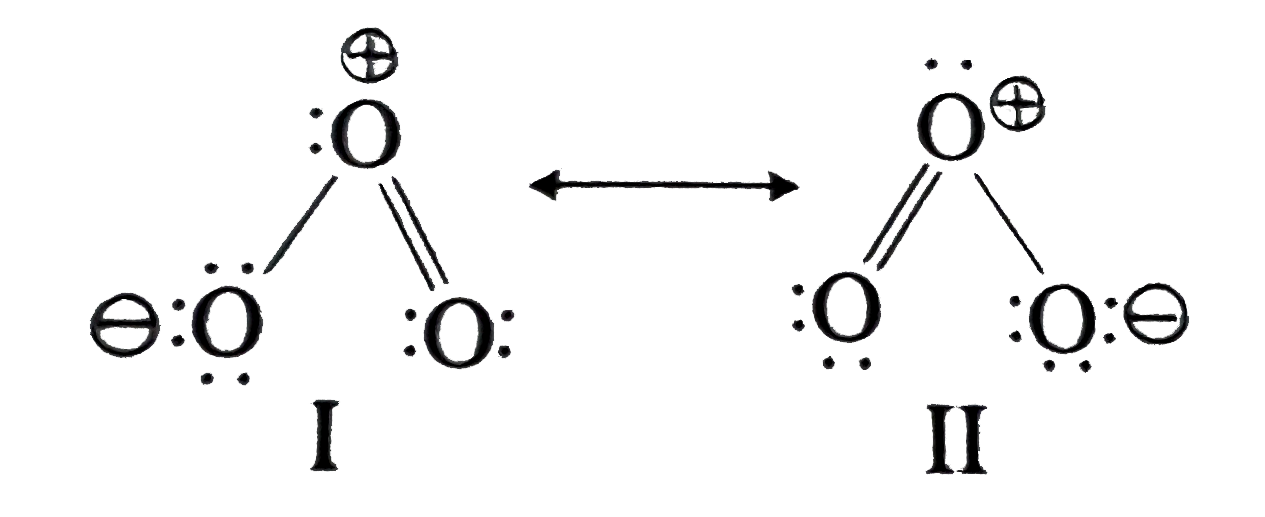
O3 exist as a hybrid of structure I and structure II Each atom may be thought as roughly sp2 hybrid.
The middle O atom has a lone pair of electrons with a delocalised π orbital over all the three oxygen atoms. The rate constant (K) of first order reaction at temp. t is given by
k=2⋅303tlogCOtt
where, CO = initial concentration, Ct = concentration after time t
For N2O5(g)→2NO2(g)+12O2(g)
CO=1⋅24×10−2mol L−1,Ct=0⋅20×10−2mol L−1t=60 min.
∴ k=2⋅30360×log1⋅24×10−2mol L−10⋅20×10−2mol L−1
=0⋅038×log(6⋅2)−1min
=0⋅038×0⋅792min−1=0⋅030min−1
Thus rate constant of the reaction at 320 K is 0⋅030 min−1.
Topper's Solved these Questions
Similar Questions
The initial concentration of N2O5 in the following first order reaction:
N2O5(g)→2NO2(g)+12O2(g)
was 1.24×10−2molL−1 at 318K. The concentration of N2O5 after 60min was 0.20×10−2molL−1. Calculate the rate constant of the reaction at 318K.
View SolutionThe initial concentration of N2O5 in the following first order reaction, N2O5(g)→2NO2(g)+12O2(g) was 1.24×10−2molL−1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20×10−2molL−1 . Calculate the rate constant of the reaction at 318 K.
View Solution
Knowledge Check
For the reaction N2O4(g)→2NO2(g)
AΔH>ΔEBΔH<ΔECΔH=ΔEDΔH=0For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)AThe concentration of the reaction decreases exponentially with timeBThe half-life of the reaction decreases with increasing temperatureCThe half-life of the reaction depends on the initial concentration of the reactantDThe reaction proceeds to 99.6 % completion in eight half-life durationThe initial concentration of N2O5 in the following order reaction, N2O5(g)→2NO2(g)+12O2(g) was 1.24×10−2 mol L−1 at 318 K. The concentration of N2O5 after 60 min was 0.20×10−2 mol L−1. Calculate the rate constant of the reaction at 318 K.
A0.0104−1minB0.0204−1minC0.0304−1minD0.0404−1min
The initial concentration of N2O5 in the following first order reaction, N2O5(g)→2NO2(g)+12O2(g) was 1.24×10−2molL−1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20×10−2molL−1 . Calculate the rate constant of the reaction at 318 K.
View SolutionThe initial concentration of N2O5 in the following first order reaction, N2O5(g)→2NO2(g)+12O2(g) was 1.24×10−2molL−1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20×10−2molL−1 . Calculate the rate constant of the reaction at 318 K.
View SolutionThe initial concentration of N2O5 in the first order reaction N2O5→2NO2+1/2O2 was 1.24×10−2mol L−1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20×10−2mol L−1. Calculate the rate constant of the reaction at 318 K.
View SolutionThe initial concentration of N2O5 in the first order reaction N2O5→2NO2+1/2O2 was 1.24×10−2mol L−1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20×10−2mol L−1. Calculate the rate constant of the reaction at 318 K.
View SolutionThe molecularity and order of the reaction 2NO(g)+O2(g)→2NO2(g) are respectively
View Solution
