The function f:x→x2−4x+k is defined for the domain x≥p, where k and p are constants. (i) Express f(x) in the form (x+a)2+b+k, where a and b are constants. (ii) State the range of f in terms of k. (iii) State the smallest value of p for which f is one-one. (iv) For the value of p found in part (iii), find an expression for f−1(x) and state the domain of f−1.giving your answer in terms of k.
Step by step video & image solution for The function f : x rarr x^2 - 4x + k is defined for the domain x ge p, where k and p are constants. (i) Express f(x) in the form (x + a)^2 + b + k, where a and b are constants. (ii) State the range of f in terms of k. (iii) State the smallest value of p for which f is one-one. (iv) For the value of p found in part (iii), find an expression for f^(-1)(x) and state the domain of f^(-1).giving your answer in terms of k. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The function f(x)=x3−ax has a local minimum at x=k, where k≥2, then a possible value of a is
A9B11C13D8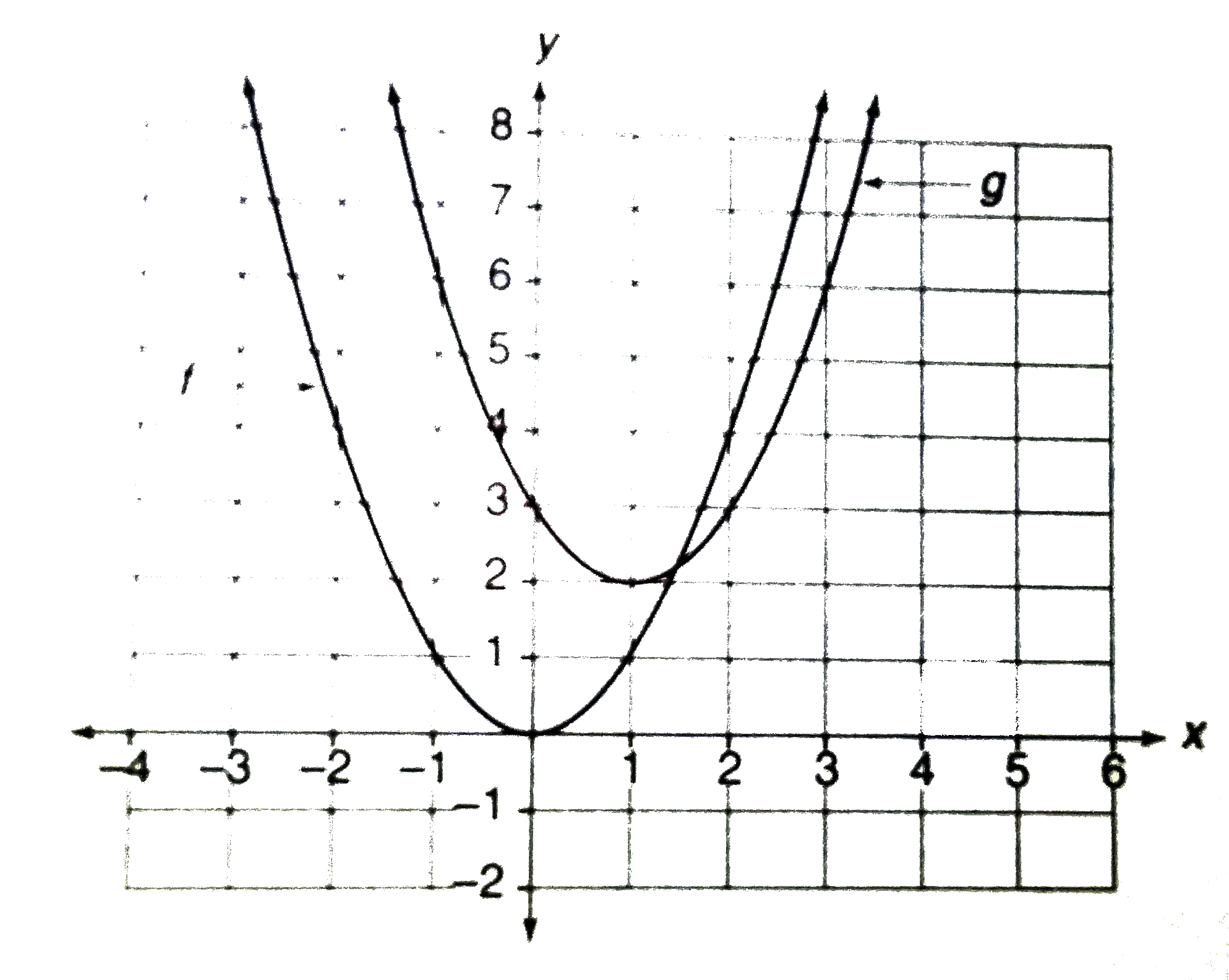
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?A−3B−2C−1D1If (x+p) is a factor of both x2+16x+64and4x2+37x+k, where p and k are nonzero integer constants, what could be the value of k?
A9B24C40D63
Let If the set of values of k for which f(x)<0∀x∈(−3,3)andf(−4)>0is(p,q) then find the value of (4p+3q), where f(x)=kx2+x(3−4k)−12.
View SolutionIn the xy-plane the point (2,5) lies on the graph of the function f. IF f(x) =k−x2 where k is a constant, what is the value of k?
View SolutionThe function f:R→B is defined by f(x)=[x]+[−x] where [.] is G.I.F. is surjective then B is
View SolutionThe function f(x)=x3−ax has a local minimum at x=k, where k≥2, then a possible value of a is
View SolutionThe function f(x) is defined by f(x)=cos4x+Kcos22x+sin4x, where K is a constant.If the function f(x) is a constant function,the value of k is
View Solution
