PQ and RS are two equal and parallel line segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. rove that line segments MN and PQ are equal and parallel to each other.
PQ||RS and PQ=RS
PQRS is a parallelogram
PR||QS and PR=QS
In∠PRN and ∠QSM
∠PRN=∠QSM
∠RPN=∠SQM
∠PRN=∠QSM
∠PRN≅∠QSM(AAA)
PR=QS
PN=QM
RN=SM
In PQMN
PN||QM and PN=QM
PQMN is a parallelogram
PQ=MN and PQ||MN.
Similar Questions
A point P lies on a line through Q(1,-2,3) and is parallel to the line x1=y4=z5. If P lies on the plane 2x+3y-4z+22=0, then segment PQ equal to
View SolutionA straight line through the origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at points P and Q respectively. Then the point O divides the segment PQ in the ratio
View SolutionA straight line through the origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at points P and Q respectively. Then the point O divides the segment PQ in the ratio :
View SolutionA point P lies on a line through Q(1, -2, 3) and is parallel to the line x1=y4=z5. If P lies on the plane 2x + 3y – 4z + 22 = 0, then segment PQ equals to
View SolutionA straight line through the origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at points P and Q respectively. Then the point O divides the segment PQ in the ratio
View Solutionरेखाखंड PQ तथा RS समांतर है इसे संकेत में व्यक्त कीजिए।
View SolutionDraw a line segment PQ. Take a point S outside this line, and draw a line parallel to PQ, through S. Join S with P. Construct a line parallel to SP, through Q. Mark the point at which it meets the parallel line through S at R. What is the shape of PQRS ?
View SolutionIn the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
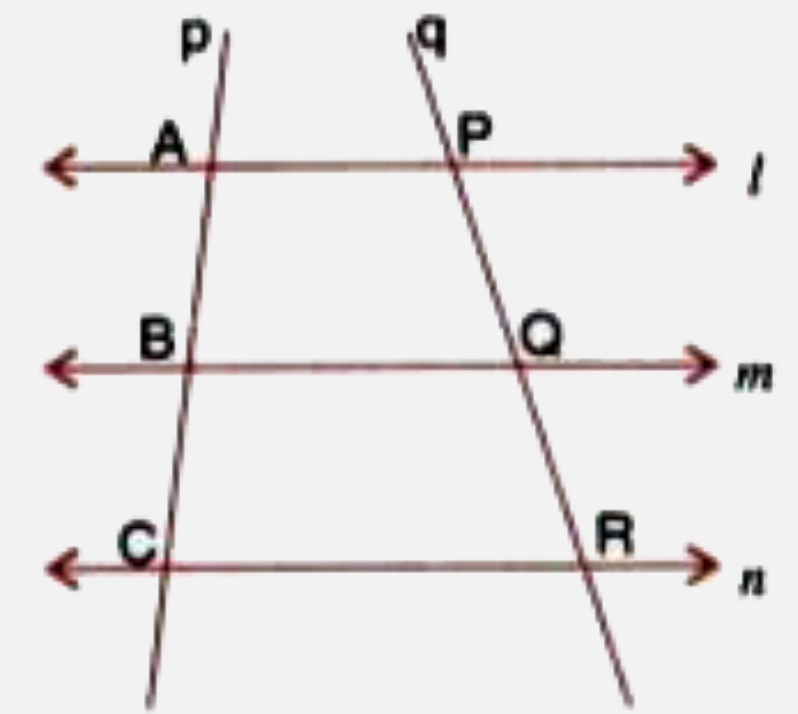
Prove that : ABBC=PQQR
Join A and R. Let AR meets BQ at point D.
View Solution
