a त्रिज्या के वृत्त से घिरे क्षेत्र का क्षेत्रफल निकालें।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

चूँकि वृत्त का क्षेत्रफल केवल त्रिज्या पर निर्भर करता है अतः वृत्त का केंद्र मूल बिंदु लिया जा सकता है।
अब वृत्त का समीकरण होगा : x2+y2=a2
अब वृत्त (1) x-अक्ष तथा कोटियों x = 0 तथा x = a से घिरे क्षेत्र का क्षेत्रफल
अर्थात क्षेत्रफल =∫a0ydx=∫a0√a2−x2dx
[∵ (1) से, वृत्त के भाग AB के लिए y=√a2−x2]
=[x√a2−x22+a22sin−1xa]a0
[∵∫√a2−x2dx=x√a2−x22+a22sin−1xa]
=0+a22sin−1(1)−(0+0)
=a22.π2=πa24
∴ वृत्त का क्षेत्रफल =4πa24=πa2 वर्ग इकाई
Second method :
क्षेत्रफल AOBA वृत्त, y - अक्ष तथा दो भुजों (abscissae ) y = 0 तथा y = a से घिरा है,
∴ वृत्त का क्षेत्रफल = 4 (AOBA का क्षेत्रफल )
=4∫a0xdy ,
=∫a0√a2−y2dy[∵x2+y2=a2∵x2=a2−y2
या x=√a2−y2, यहाँ x>0]
=4[y√a2−y22+a22sin−1ya]a0
=4[{0+a22sin−1(1)}−(0+0)]
=4.a22.π2 [∵sin−1(1)=π2]
=πa2 वर्ग इकाई
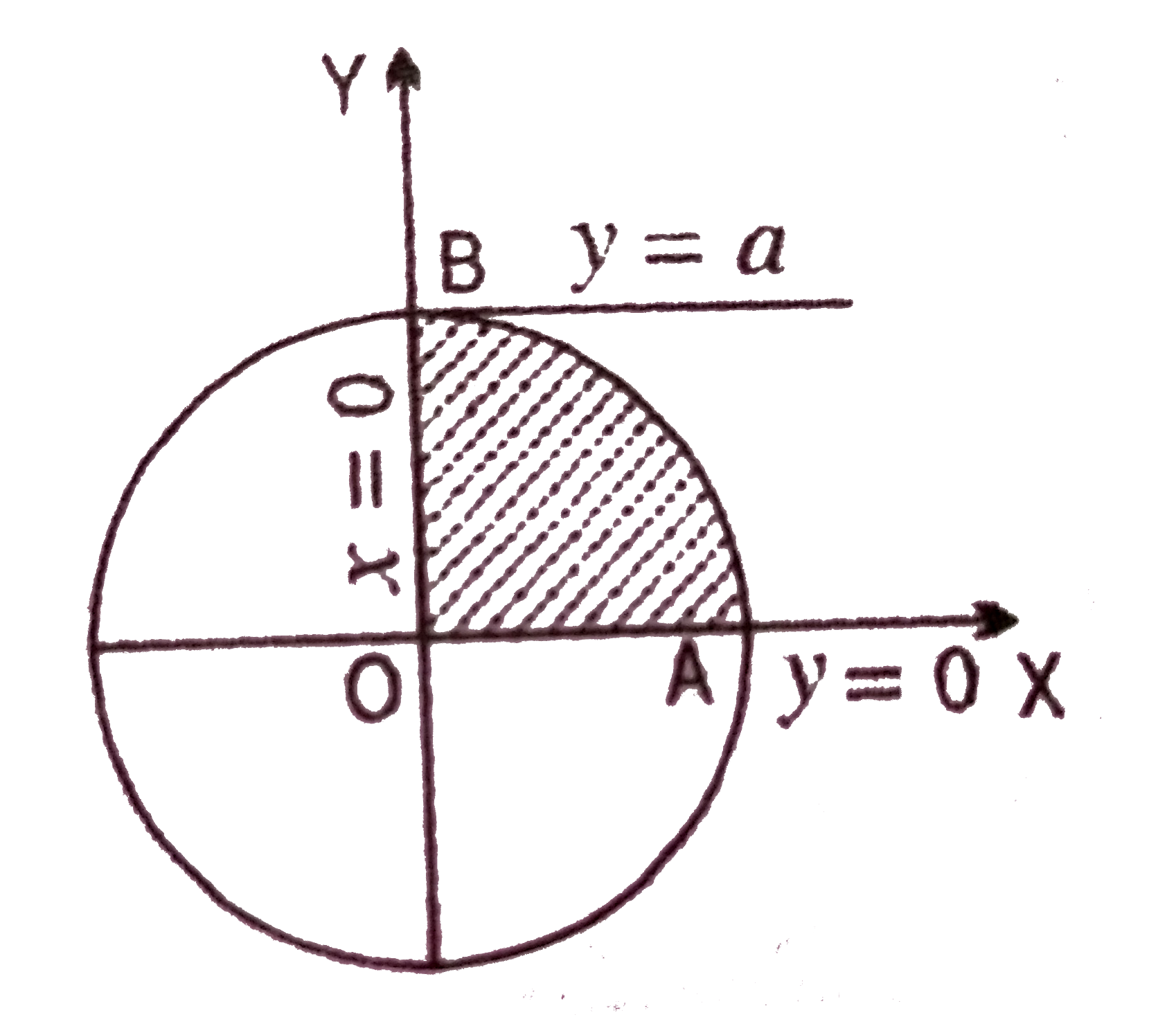
ocr_image
ocr_image

Updated on:21/07/2023
|
Class 12MATHSAPPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions