पासो के एक जोड़े को तीन बार उछाला जाता है। यदि यादृच्छिक चर X द्विको की संख्या है, तो X का प्रायिकता बंटन ज्ञात करें।
माना कि यादृच्छिक चर (द्विको की संख्या) X है।
X के संभव मान 0, 1, 2 है।
माना कि E = पासे के एक जोड़े को एक बार उछालने पर द्विक आने की घटना
तो P(E)=636=16⇒P(¯¯¯E)=1−P(E)=56
अब P(X=0)=P(¯¯¯E1¯¯¯E2)=P(¯¯¯E1)P(¯¯¯E2)=56×56=2536
P(X=1)=P(E1¯¯¯E2 या, ¯¯¯E1E2)=P(E1¯¯¯E2)+P(¯¯¯E1E2)
=P(E1)P(¯¯¯E2)+P(¯¯¯E1)P(E2)
=16×56+56×16=1036
P(X=2)=P(E1E2)=P(E1)P(E2)
=16×16=136
अतः X का प्रायिकता बंटन है : X012P(X)25361036136
Topper's Solved these Questions
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type I.
7 Videos
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type II.
16 Videos
- बरनौली परीक्षण और द्विपद बंटन BOOK - KC SINHACHAPTER - बरनौली परीक्षण और द्विपद बंटन EXERCISE - OBJECTIVE QUESTIONS
10 Videos
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - OBJECTIVE QUESTIONS
5 Videos
Similar Questions
X012P(X)0.20.60.2
View Solutionदो सिक्को के एक साथ उछाल में यादृच्छिक चर पटो की संख्या X का प्रायिकता बंटन ज्ञात कीजिए।
View SolutionIn a box containing 100 bulbs , 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective ?
View SolutionThe corner pont sof the feasible region determined by the followign system of linear inequalities :2x+y≤10,x+3y≤15,xy≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy where p,q≥0. Conditions on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is
View Solutionयदि यादृच्छिक चर X के संगत प्रायिकता P(X) हो , तो घटना E का X माध्य E(X) = ……….. होगा।
View Solutionयदि यादृच्छिक चरX के संगत प्रायिकता P(X) हो , तो X का प्रसरण Var(X)=……… होगा।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - 4 सफलता के लिए
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionदो पासो को एक साथ चार बार फेका जाता है दोनों पासो पर प्राप्त अंको का योग 7 कम से कम दो बार आने की प्रायिकता ज्ञात कीजिए
View Solutionएक पासा 5 बार फेका जाता है यदि विषम संख्या प्राप्त होने को के सफलता माना जाए तो प्रायिकता ज्ञात कीजिए - चार सफलताएं प्राप्त हो
View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
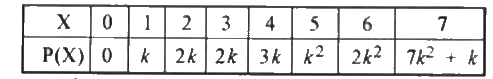ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)
View Solutionयदि एक निष्पक्ष सिक्के को 20 बार उछला जाता है और मान लीजिये कि n बार शीर्ष दिखाई देता है, तो n के विषम होने की प्रायिकता का मान ज्ञात कीजिए।
View Solutionयदि एक न्याय्य सिक्के को 10 बार उछला जाता है, ठीक चार पट आने की प्रायिकता ज्ञात कीजिए।
View Solutionएक काले तथा लाल पासे को कर्म में उछाला गया है। तब
पासो पर प्राप्त अंको का योग 9 से अधिक होने कि सप्रतिबन्ध प्रायिकता ज्ञात करो यदि ज्ञात है कि काले पासे पर अंक 5 प्रकट हुआ है।
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionपाँच पासो को एक साथ फेंका गया है। यदि एक पासे पर सम अंक आने को सफलता माना जाये तो अधिकतम 3 सफलताओ कि प्रायिकता ज्ञात करो ।
View Solution