यदि (3z+10) बहुपद 9z3−27z2−100z+300 का एक गुणनखण्ड है, तो इसके गुणनखण्ड ज्ञात कीजिए ।
आइए 9z3−27z2−100z+300 के अन्य गुणनखण्ड प्राप्त करने के लिये दिये बहुपद को 3z+10 से विभाजित करते हैं।
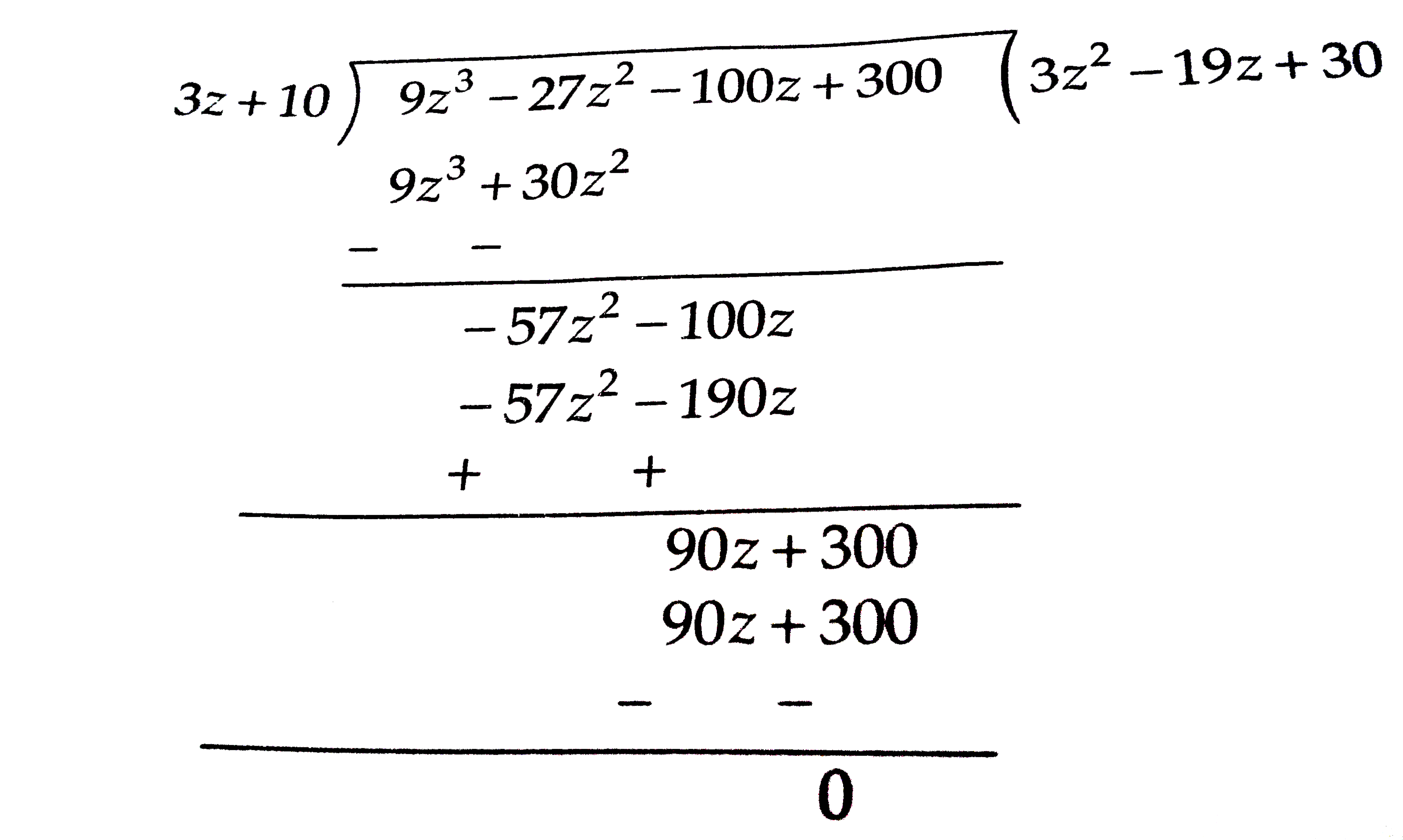
∴ 9z3−27z2−100z+300
=(3z+10)(3z2−19z+30)
=(3z+10)(3z2−10z−9z+30)
=(3z+10){(3z2−10z)−(9z−30)}
=(3z+10){z(3z−10)−3(3z−10)}
=(3z+10)(3z−10)(z−3)
अतः 9z3−27z2−100z+300=(3z+10)(3z−10)(z−3)
वैकल्पिक विधि : दिया है,
9z3−27z2−100z+300
=3z2(3z+10)−19z(3z+10)+30(3z+10) [∵3z+10 बहुपद का एक गुणनखण्ड है।]
=(3z+10)(3z2−19z+30)
=(3z+10){3z2−10z−9z+30}
=(3z+10){z(3z−10)−3(3z−10)}
=(3z+10)(3z−10)(z−3)
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - बहुपदों का गुणनखण्डनEXERCISE - प्रश्नावली 6.137videos
बहुपदों का गुणनखण्डन
- BOOK - RD SHARMACHAPTER - बहुपदों का गुणनखण्डनEXERCISE - प्रश्नावली 6.210videos
बहुपदों का गुणनखण्डन
- BOOK - RD SHARMACHAPTER - प्रायिकता EXERCISE - बहु विकल्पीय प्रश्न10videos
प्रायिकता
- BOOK - RD SHARMACHAPTER - बीजीय व्यंजको का गुणनखण्डन EXERCISE - बहु विकल्पीय प्रश्न15videos
बीजीय व्यंजको का गुणनखण्डन
Similar Questions
निम्नलिखित व्यंजकों में कौन-सा व्यंजक एक चर वाला बहुपद है? कारण के साथ बताइये?
3x2−4x+1503:02View Solutionयदि f(x)=2x3−13x2+17x+12 हो, तो (i) f(2)(ii) f(−3)(iii) f(0) ज्ञात कीजिए ।
05:08View Solutionकिसी घटना A के घटित होने कि प्रायिकता P(A) के लिए निम्न में से कौन - सा कथन सत्य है :
02:36View Solutiona2−1−2x−x2 के गुणनखण्ड होंगे:
05:31View SolutionFactorize 9z3−27z2−100z+300, if it is given that (3z+10) is a factor of it.
06:58View SolutionFactorize 9z3−27z2−100z+300; if it is given that (3z+10) is a factor it.
03:45View Solutionयदि 9 सेमी ऊँचाई वाले एक लंबवृत्तीय शंकु का आयतन 48π सेमी^(3) गहरा है, तो इसके आधार का व्यास ज्ञात कीजिए ?
03:12View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
04:21View Solutionदो बहुपदो का लघुतम समापवर्तक x3−6x2+3x+10 है तथा महत्तम समापवर्तक (x+1) है। यदि एक बहुपद x2−4x−5 है तो दूसरा बहुपद ज्ञात कीजिये।
02:51View Solutionयदि y=1−cos2x1+cos2x है तो dydx का मान ज्ञात कीजिए।
View Solutionएक रेखा बिंदु 2ˆi+ˆj−3ˆk से गुजरती है और साधीश ˆi+2ˆj+ˆk के समांतर है । रेखा का सदिश समाकरण ज्ञात कीजिए। इसके द्वारा रेखा का कार्तीय समीकरण ज्ञात कीजिए।
03:43View Solutionयदि निम्न बंटन का माध्य 50 है तो लुप्त बारंबारताएं ज्ञात कीजिए।
 03:24View Solution
03:24View Solutionबहुपद 2x3+x2−5x+2के अन्य शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक 1 और-2 हैं। ज्ञात कीजिए,
01:49View Solutionक्या 3x + 10, बहुपद9x^(3)-27x^(2)-100x+300 का गुणनखण्ड है ?
44:34View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
01:24View Solution

