From the prices of shares X and Y below, find out which is more stable in value
To determine which share, X or Y, is more stable in value, we will calculate the coefficient of variation (CV) for both shares. The share with the lower CV will be considered more stable.
Step 1: Calculate the Mean of Shares X and Y
1. Mean of X (X̄):
- Given prices of share X: 8, 50, 51, 52, 53, 54, 55, 56, 57, 58
- Mean (X̄) = (Sum of all prices) / (Number of prices)
- Mean (X̄) = (8 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58) / 10
- Mean (X̄) = 405 / 10 = 51
2. Mean of Y (Ȳ):
- Given prices of share Y: 1, 3, 4, 5, 1, 3, 5, 1, 5, 1
- Mean (Ȳ) = (Sum of all prices) / (Number of prices)
- Mean (Ȳ) = (1 + 3 + 4 + 5 + 1 + 3 + 5 + 1 + 5 + 1) / 10
- Mean (Ȳ) = 30 / 10 = 3
Step 2: Calculate the Variance and Standard Deviation of Shares X and Y
1. Variance of X:
- Variance (σ²) = (Sum of (Xᵢ - X̄)²) / N
- Deviations for X:
- (8 - 51)² = 1849
- (50 - 51)² = 1
- (51 - 51)² = 0
- (52 - 51)² = 1
- (53 - 51)² = 4
- (54 - 51)² = 9
- (55 - 51)² = 16
- (56 - 51)² = 25
- (57 - 51)² = 36
- (58 - 51)² = 49
- Sum of deviations = 1849 + 1 + 0 + 1 + 4 + 9 + 16 + 25 + 36 + 49 = 1990
- Variance of X = 1990 / 10 = 199
2. Variance of Y:
- Variance (σ²) = (Sum of (Yᵢ - Ȳ)²) / N
- Deviations for Y:
- (1 - 3)² = 4
- (3 - 3)² = 0
- (4 - 3)² = 1
- (5 - 3)² = 4
- (1 - 3)² = 4
- (3 - 3)² = 0
- (5 - 3)² = 4
- (1 - 3)² = 4
- (5 - 3)² = 4
- (1 - 3)² = 4
- Sum of deviations = 4 + 0 + 1 + 4 + 4 + 0 + 4 + 4 + 4 + 4 = 29
- Variance of Y = 29 / 10 = 2.9
Step 3: Calculate the Standard Deviation
1. Standard Deviation of X (σₓ):
- σₓ = √Variance of X = √199 ≈ 14.1
2. Standard Deviation of Y (σᵧ):
- σᵧ = √Variance of Y = √2.9 ≈ 1.7
Step 4: Calculate the Coefficient of Variation (CV)
1. Coefficient of Variation for X (CVₓ):
- CVₓ = (σₓ / X̄) * 100
- CVₓ = (14.1 / 51) * 100 ≈ 27.65%
2. Coefficient of Variation for Y (CVᵧ):
- CVᵧ = (σᵧ / Ȳ) * 100
- CVᵧ = (1.7 / 3) * 100 ≈ 56.67%
Step 5: Compare the Coefficient of Variation
- CVₓ ≈ 27.65%
- CVᵧ ≈ 56.67%
Since CVₓ < CVᵧ, share X is more stable than share Y.
Conclusion
Thus, share X is more stable in value compared to share Y.
---
- Given prices of share X: 8, 50, 51, 52, 53, 54, 55, 56, 57, 58
- Mean (X̄) = (Sum of all prices) / (Number of prices)
- Mean (X̄) = (8 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58) / 10
- Mean (X̄) = 405 / 10 = 51
- Given prices of share Y: 1, 3, 4, 5, 1, 3, 5, 1, 5, 1
- Mean (Ȳ) = (Sum of all prices) / (Number of prices)
- Mean (Ȳ) = (1 + 3 + 4 + 5 + 1 + 3 + 5 + 1 + 5 + 1) / 10
- Mean (Ȳ) = 30 / 10 = 3
- Variance (σ²) = (Sum of (Xᵢ - X̄)²) / N
- Deviations for X:
- (8 - 51)² = 1849
- (50 - 51)² = 1
- (51 - 51)² = 0
- (52 - 51)² = 1
- (53 - 51)² = 4
- (54 - 51)² = 9
- (55 - 51)² = 16
- (56 - 51)² = 25
- (57 - 51)² = 36
- (58 - 51)² = 49
- Sum of deviations = 1849 + 1 + 0 + 1 + 4 + 9 + 16 + 25 + 36 + 49 = 1990
- Variance of X = 1990 / 10 = 199
- Variance (σ²) = (Sum of (Yᵢ - Ȳ)²) / N
- Deviations for Y:
- (1 - 3)² = 4
- (3 - 3)² = 0
- (4 - 3)² = 1
- (5 - 3)² = 4
- (1 - 3)² = 4
- (3 - 3)² = 0
- (5 - 3)² = 4
- (1 - 3)² = 4
- (5 - 3)² = 4
- (1 - 3)² = 4
- Sum of deviations = 4 + 0 + 1 + 4 + 4 + 0 + 4 + 4 + 4 + 4 = 29
- Variance of Y = 29 / 10 = 2.9
- σₓ = √Variance of X = √199 ≈ 14.1
- σᵧ = √Variance of Y = √2.9 ≈ 1.7
- CVₓ = (σₓ / X̄) * 100
- CVₓ = (14.1 / 51) * 100 ≈ 27.65%
- CVᵧ = (σᵧ / Ȳ) * 100
- CVᵧ = (1.7 / 3) * 100 ≈ 56.67%
- CVᵧ ≈ 56.67%
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following is more stable?
ASi4+BSn4+CGe4+DPb4+Some pairs of ions are given below. In which pair, first ion is more stable than second ?
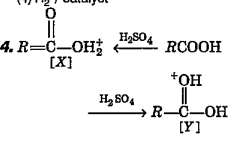
ACH3−⊕CH−CH3andCH3−⊕CH−OCH3BCH3−CH2−⊕CH−CH3andCH2=CH−CH2−⊕CH2C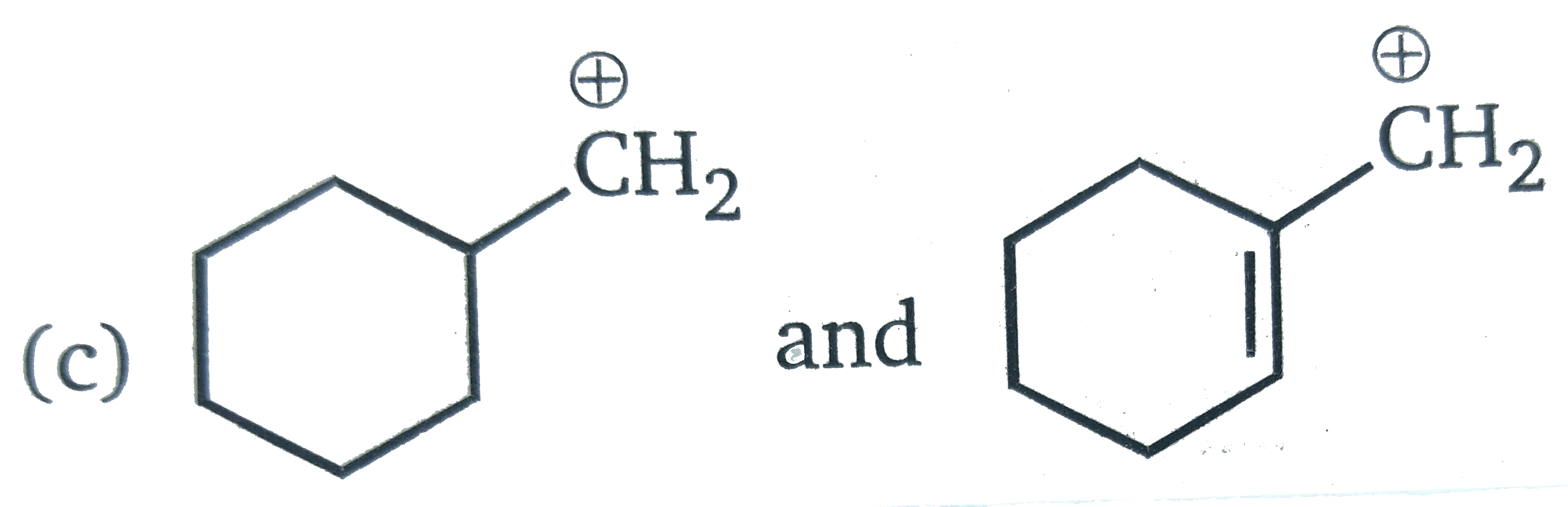 D
D
Find the more stable C⊕?
A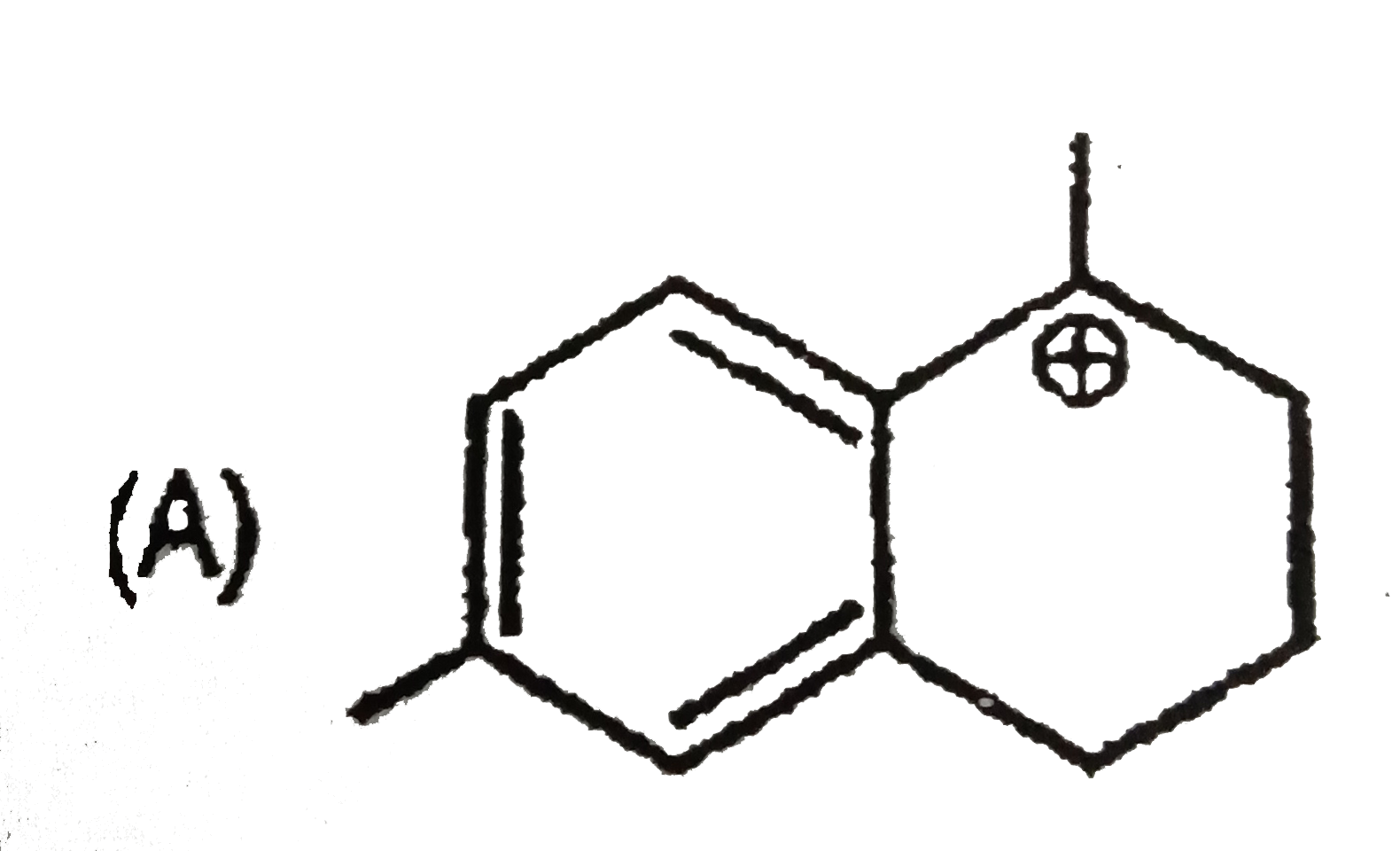 B
B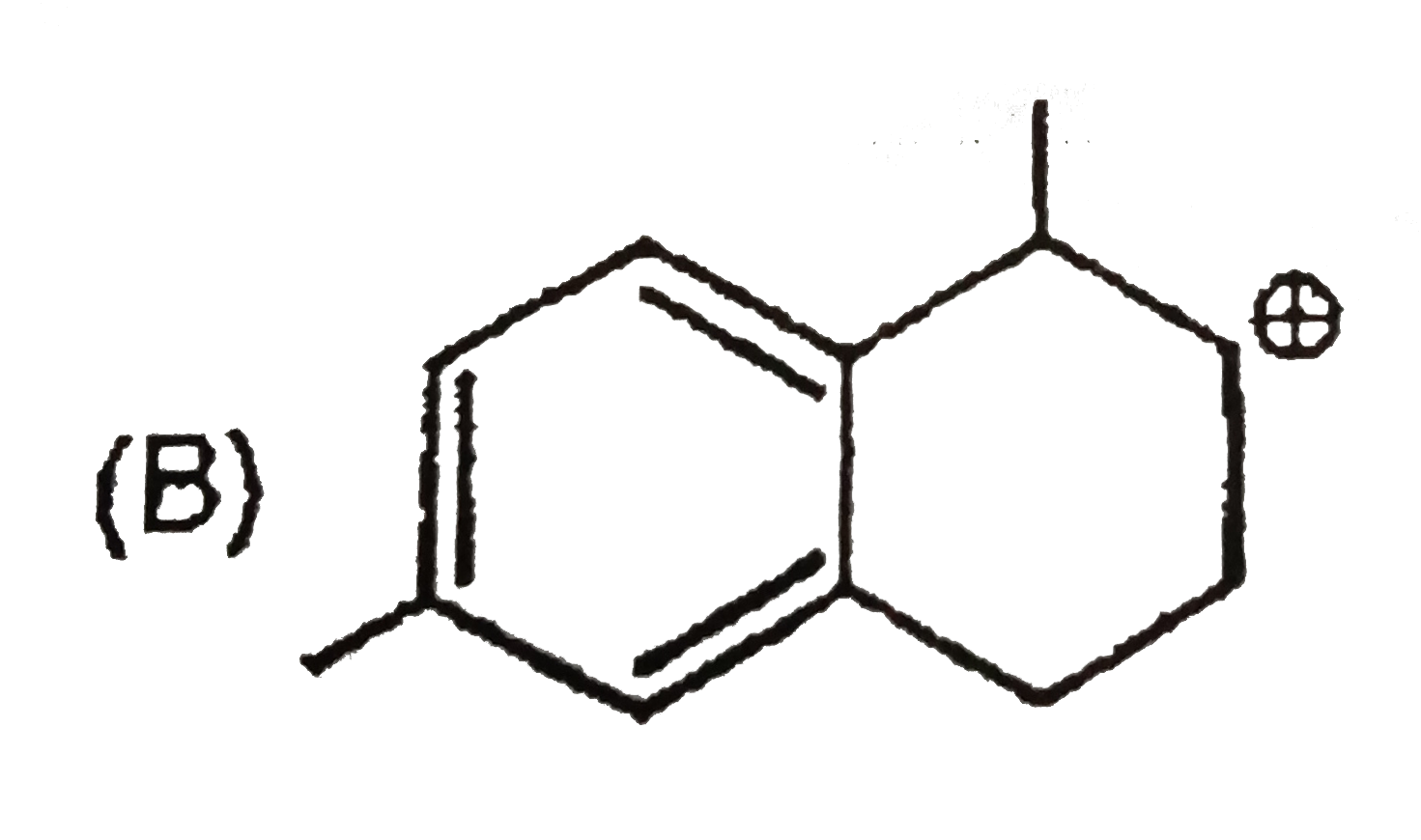 C
C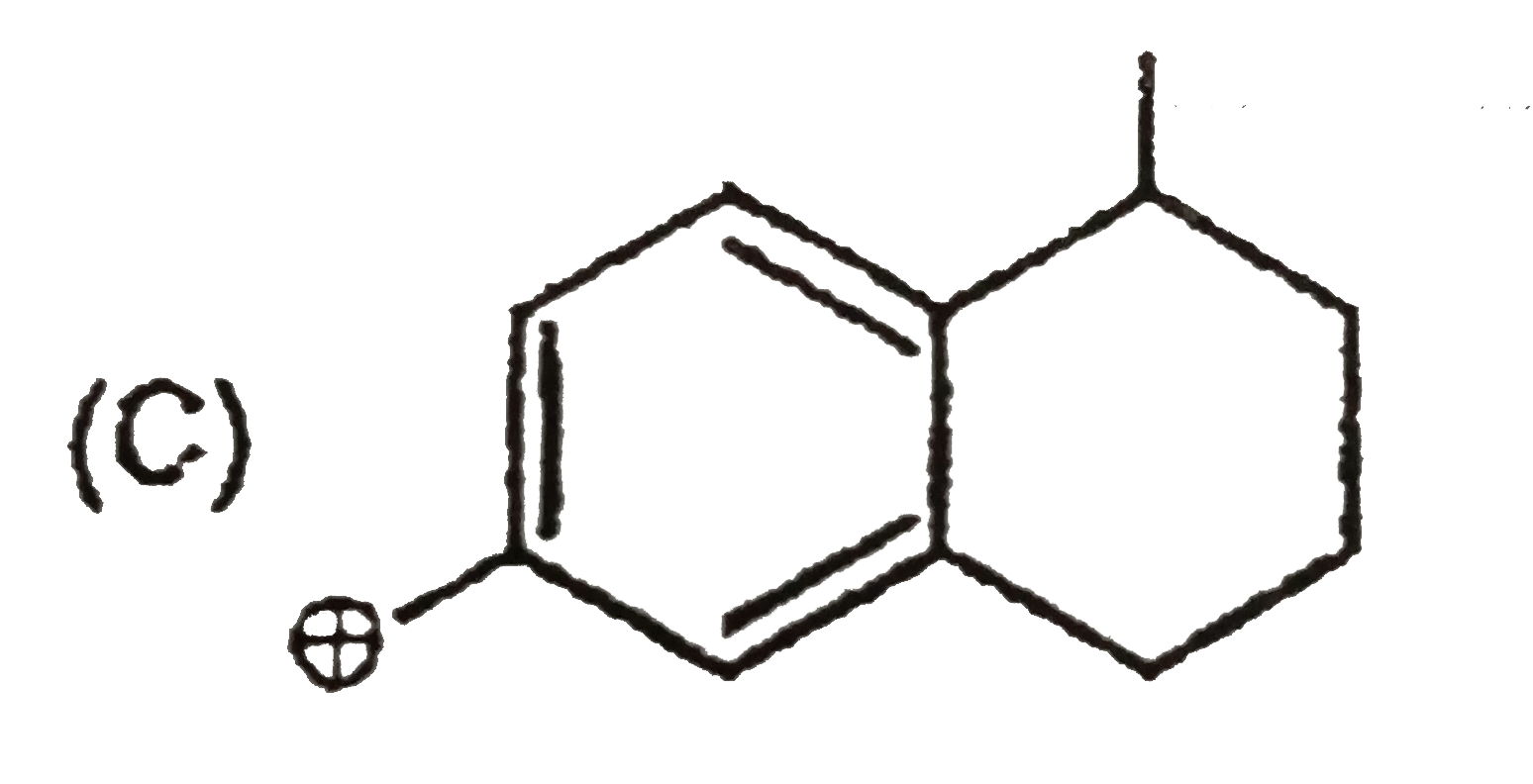 D
D
Which of the following ions is more stable ?
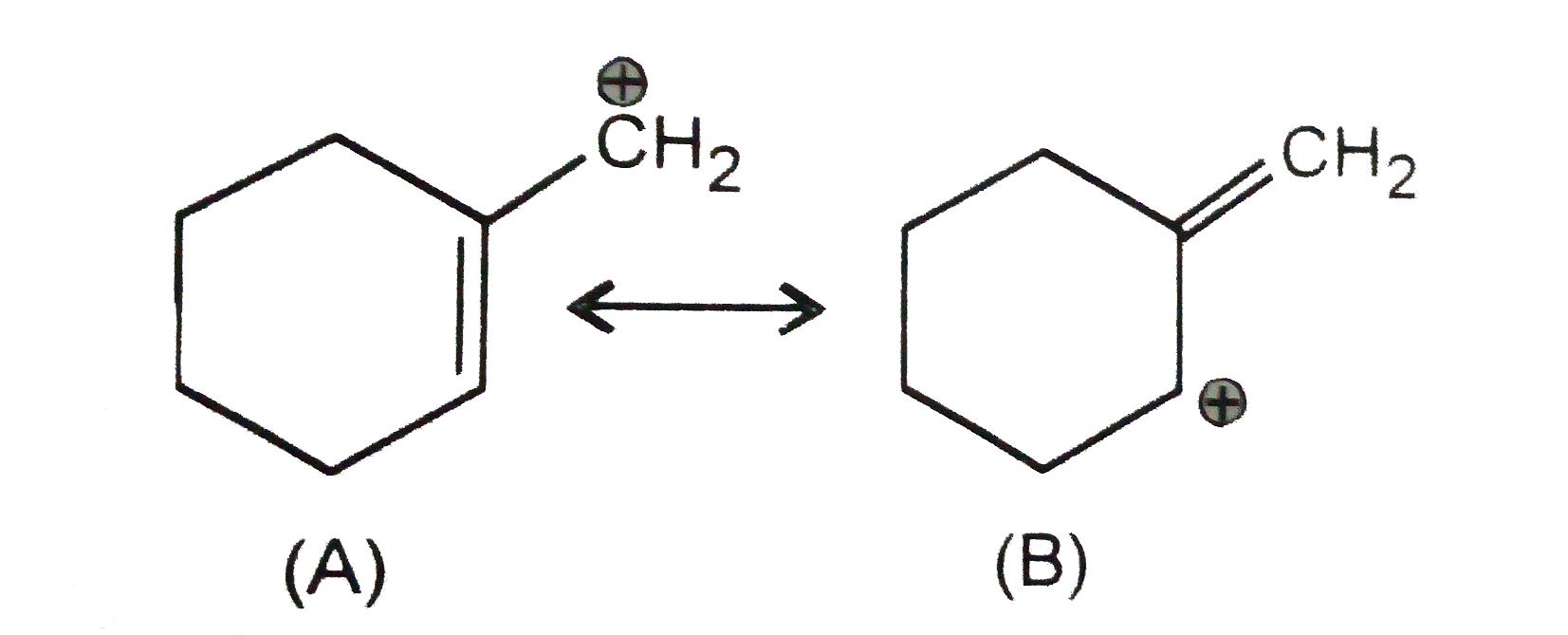
View SolutionWhich of the following ions is more stable ?
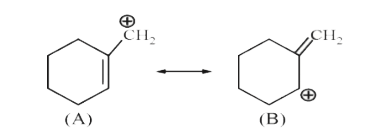
View SolutionOut of benzyl and ethyl carbocation which is more stable?
View SolutionOut of boat and chair form of cyclohexane, which is more stable ?
View SolutionOut of Fe2+ and Fe3+ ions, which is more stable ?
View Solution