What is the slope of following straight lines corresponding to equations
(a) y=2x
(b) y=−6x
(c) y=4x+2
(d) y=6x−4
A
2 , −6 , 4 , 6
B
2 , −6 , 4 , 2
C
3 , −6 , 4 , 6
D
2 , −6 , 2 , 6
Video Solution
Text Solution
The correct Answer is:A
(a) In y=2x , slops is 2 and intercept is zero . Hence, the graph is as shows below.
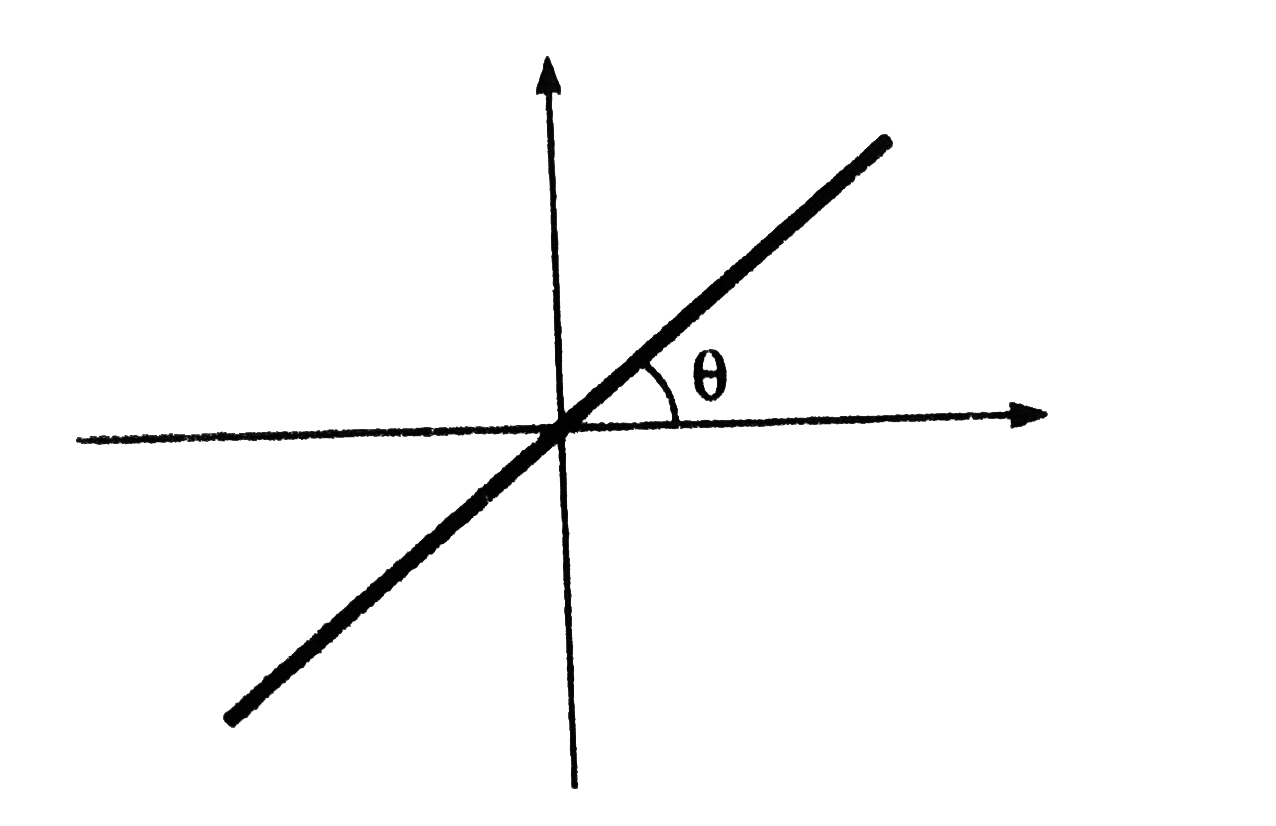
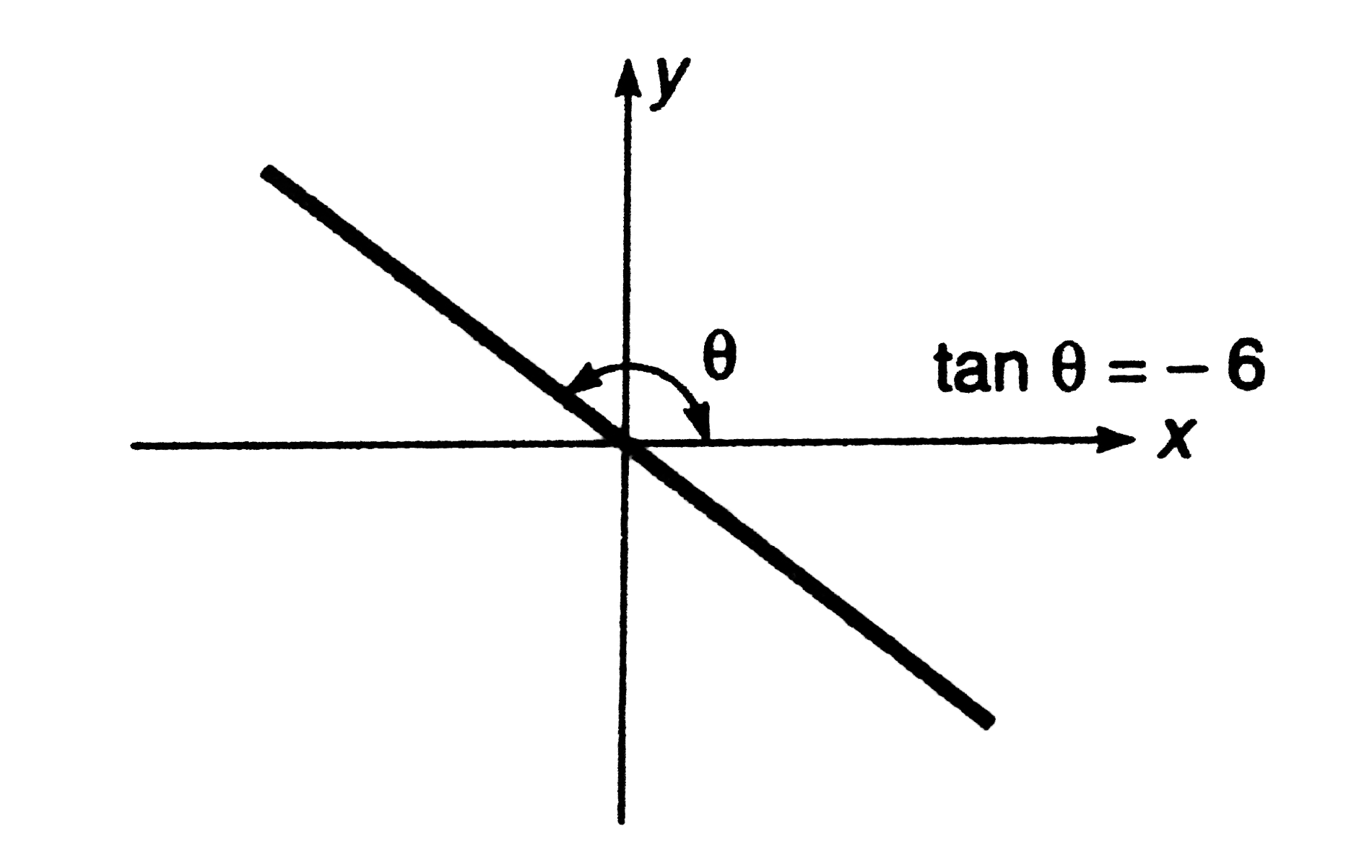
(b) In y=−6x , slope is −6 and intercept is zero . Hence , the graph is as shows below.
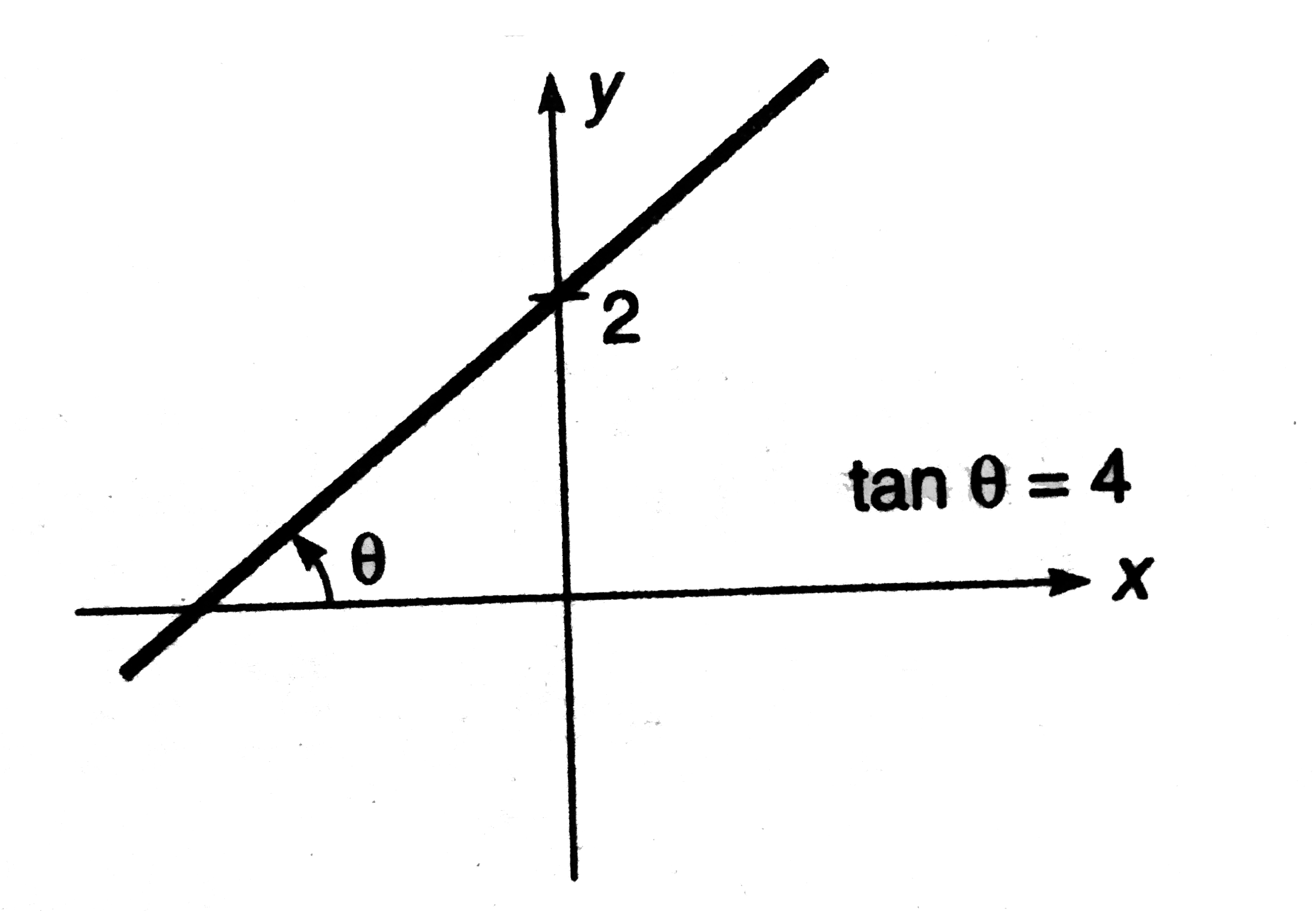
(c) In y=4x+2 , slope is +4 and intercept is 2 . The graph is as shows below.
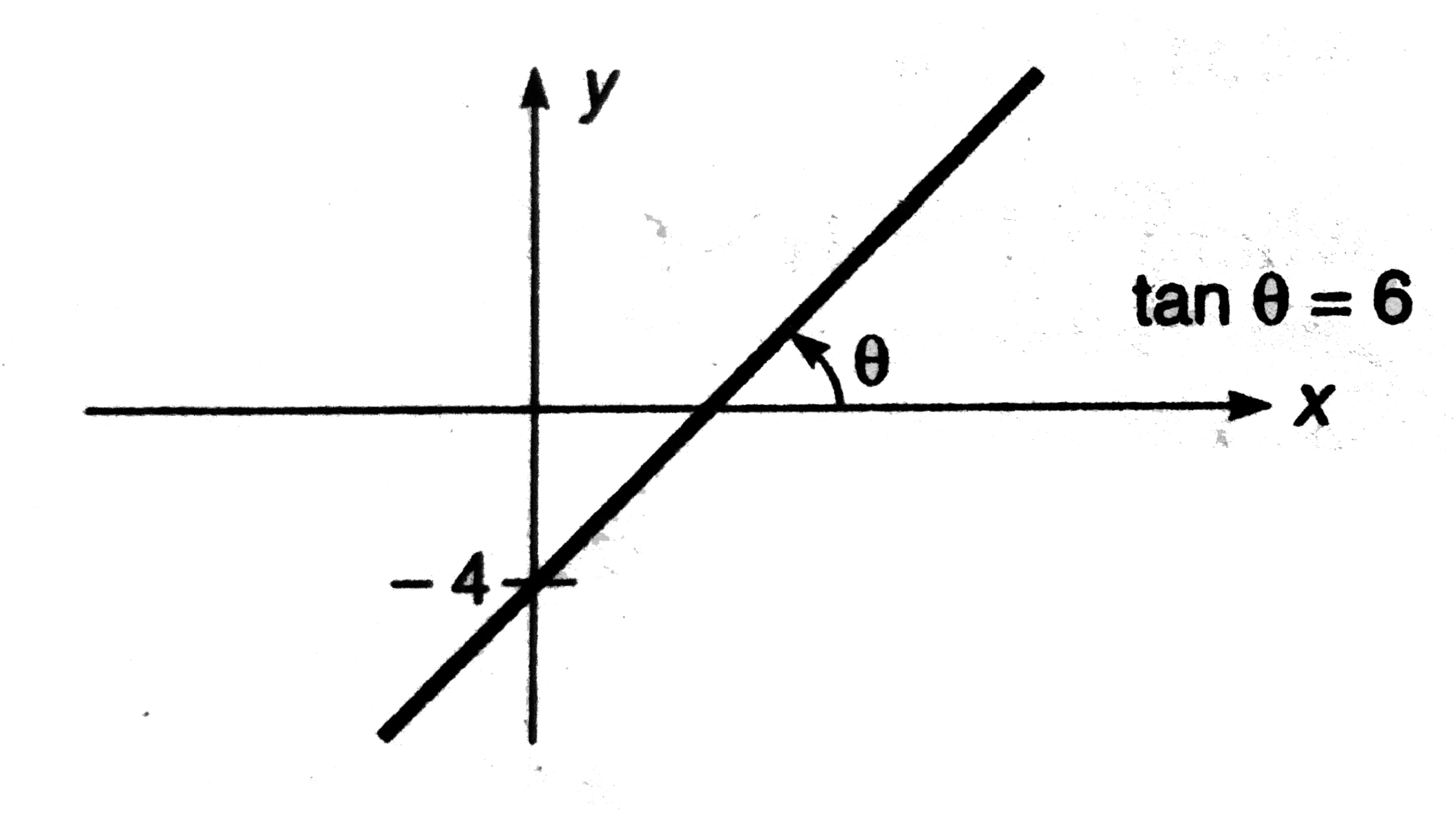
 (d) In y=6x−4 , slope is +6 and intercept is −4. Hence, the graph is as shows below.
(d) In y=6x−4 , slope is +6 and intercept is −4. Hence, the graph is as shows below.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two straight line paths are represented by the equations 2x -y = 2 and -4x + 2y = 6 . Then , the paths will
ACross each other at one pointBNot cross each otherCCross each other at two pointsDCross each other at infinitely many pointsThe distance between the lines 4x + 3y = 11 and 8x + 6y = 15 is
A3/2B3/10C6D5What is the equation of straight line pass through the point of intersection of the line x2+y3=1 and x3+y2=1 , and parallel the line 4x + 5y - 6 = 0 ?
A20x+25y−54=0B25 x + 20 y - 54 = 0C4x + 5y - 54 = 0D4x + 5y - 45 = 0
Solve the following pairs of equations
(i) x+y=3.3, 0.63x−2y=−1,3x−2y≠0
(ii) x3+y4=4, 5x6−y8=4
(iii) 4x+6y=15, 6x−8y=14,y≠0
(iv) 12x−1y=−1, 1x+12y=8,x,y≠0
(v) 43x+67y=−24, 67x+43y=24
(vi) xa+yb=a+b, xa2+yb2=2,a,b≠0
(vii) 2xyx+y=32, xy2x−y=−310,x+y≠0,2x−y≠0
View SolutionFor the equations given below, tell the nature of graphs.
(a) y=2x2 (b) y=−4x2+6
(c) y=6−4x (d) y=4(1−e−2x)
(e) y=4x (f) y=−2x
View SolutionTwo straight line paths are represented by the equation 2x−y=2 and −4x+2y=6. Then the paths will
View SolutionFind the value of λ , if the line x−3y+4+λ(8x−3y+2)=0 is parallel to the X-axis .
View SolutionWhat is the value of λ if the straight line (2x+3y+4)+λ(6x−y+12)=0 is parallel to y axis?
View Solution
