To find index error e distance between object needle and poler of the concave mirror is 20cm. The separation between the indices of object needle and mirror was observed to be 20.2cm in some observation, the observed image distance is 20.2cm and the object distance is 30.2cm find
(a) the index error e.
(b) focal length of the mirror f.
The correct Answer is:A, B, C
To solve the problem step by step, we will find the index error e and the focal length f of the concave mirror.
Step 1: Calculate the Index Error e
The index error is defined as the difference between the observed value and the actual value.
Given:
- Observed distance between the object needle and the pole of the mirror = 20.2 cm
- Actual distance between the object needle and the pole of the mirror = 20 cm
Using the formula:
e=Observed value−Actual value
Substituting the values:
e=20.2cm−20cm=0.2cm
Step 2: Calculate the Actual Image Distance v
The observed image distance is given as 20.2 cm. To find the actual image distance, we subtract the index error from the observed image distance.
Given:
- Observed image distance = 20.2 cm
Using the formula:
Actual image distance=Observed image distance−e
Substituting the values:
v=20.2cm−0.2cm=20cm
Step 3: Calculate the Actual Object Distance u
The observed object distance is given as 30.2 cm. To find the actual object distance, we subtract the index error from the observed object distance.
Given:
- Observed object distance = 30.2 cm
Using the formula:
Actual object distance=Observed object distance−e
Substituting the values:
u=30.2cm−0.2cm=30cm
Step 4: Apply the Mirror Formula to Find the Focal Length f
The mirror formula is given by:
1f=1v+1u
Since we are dealing with a concave mirror, both u and v will be negative:
- v=−20cm
- u=−30cm
Substituting the values into the mirror formula:
1f=1−20+1−30
Finding a common denominator (which is 60):
1f=−360+−260=−560
Taking the reciprocal to find f:
f=−605=−12cm
Final Answers
(a) The index error e=0.2cm
(b) The focal length of the mirror f=−12cm
---
- Observed distance between the object needle and the pole of the mirror = 20.2 cm
- Actual distance between the object needle and the pole of the mirror = 20 cm
e=Observed value−Actual value
Substituting the values:
e=20.2cm−20cm=0.2cm
- Observed image distance = 20.2 cm
Actual image distance=Observed image distance−e
Substituting the values:
v=20.2cm−0.2cm=20cm
- Observed object distance = 30.2 cm
Actual object distance=Observed object distance−e
Substituting the values:
u=30.2cm−0.2cm=30cm
1f=1v+1u
- v=−20cm
- u=−30cm
1f=1−20+1−30
1f=−360+−260=−560
f=−605=−12cm
(a) The index error e=0.2cm
Topper's Solved these Questions
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.1
2 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.2
2 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
Similar Questions
In some observation the observed object distance (Separation between indicos of object needle and mirror) is 30.2cm and the observed imager distane is 19.9cm Using index correction from previous two questions estimate the focal length of the concave mirror .
View SolutionThe distance between the object and its image formed by a plane mirror appears to be 24 cm. What is the distance between the mirror and the object?
View Solution
Knowledge Check
To find index error for u when a knitting needle of length 20.0cm is adjusted between pole and object needle the separation between the indices of object needle and mirror was pbserved to be 20.2cm Index correction for u is .
A−0.2cmB0.2cmC−0.1cmD0.1cmTo find index error v when the same knitting needle is adjusted between the pole and the image needle the separation between the indices of image needle and mirror was found to be 19.9cm Index error for v is .
A0.1cmB−0.1cmC0.2cmD−0.2cmAn object is placed 40 cm from the concave mirror with a focal length of 20 cm. The image formed is:
Abehind the mirrorBbetween the mirror and focusCat focusDcentre of curvature of mirror
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is kept at a distance 20 cm from a convex mirror of focal length 20 cm. The image will form at
View SolutionAn object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
View SolutionWhat is the distance of an object from a concave mirror of focal length 20 cm so that the size of the real image is three times the size of the object ?
View SolutionIn u−v method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices A and B. (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.
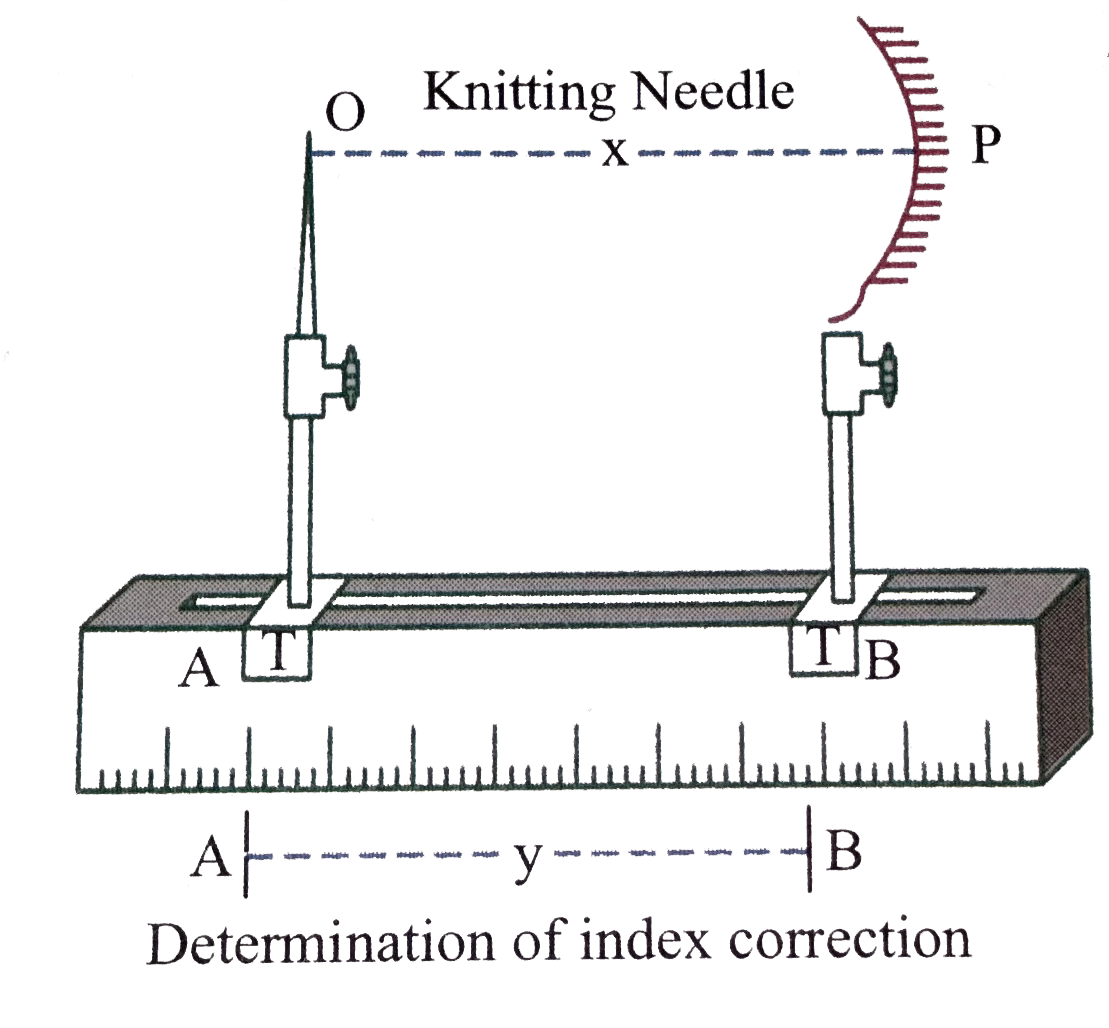
Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle O. The length of knitting needle will give the actual object distance while the seperation between indices A and B at that instant is the observed distance.
So index error is-
e=Observed distance-Actual distance
= Separation between indices A and B- Length of knitting neddle once we get e, in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
In some observation, the observed object distance (Separation between indices of object needle and mirror) is 30.2cm, and the observed image distance is 19.9cm. Using index correction from previous two equations, estimate the focal distance of the concave mirror!
View Solution
