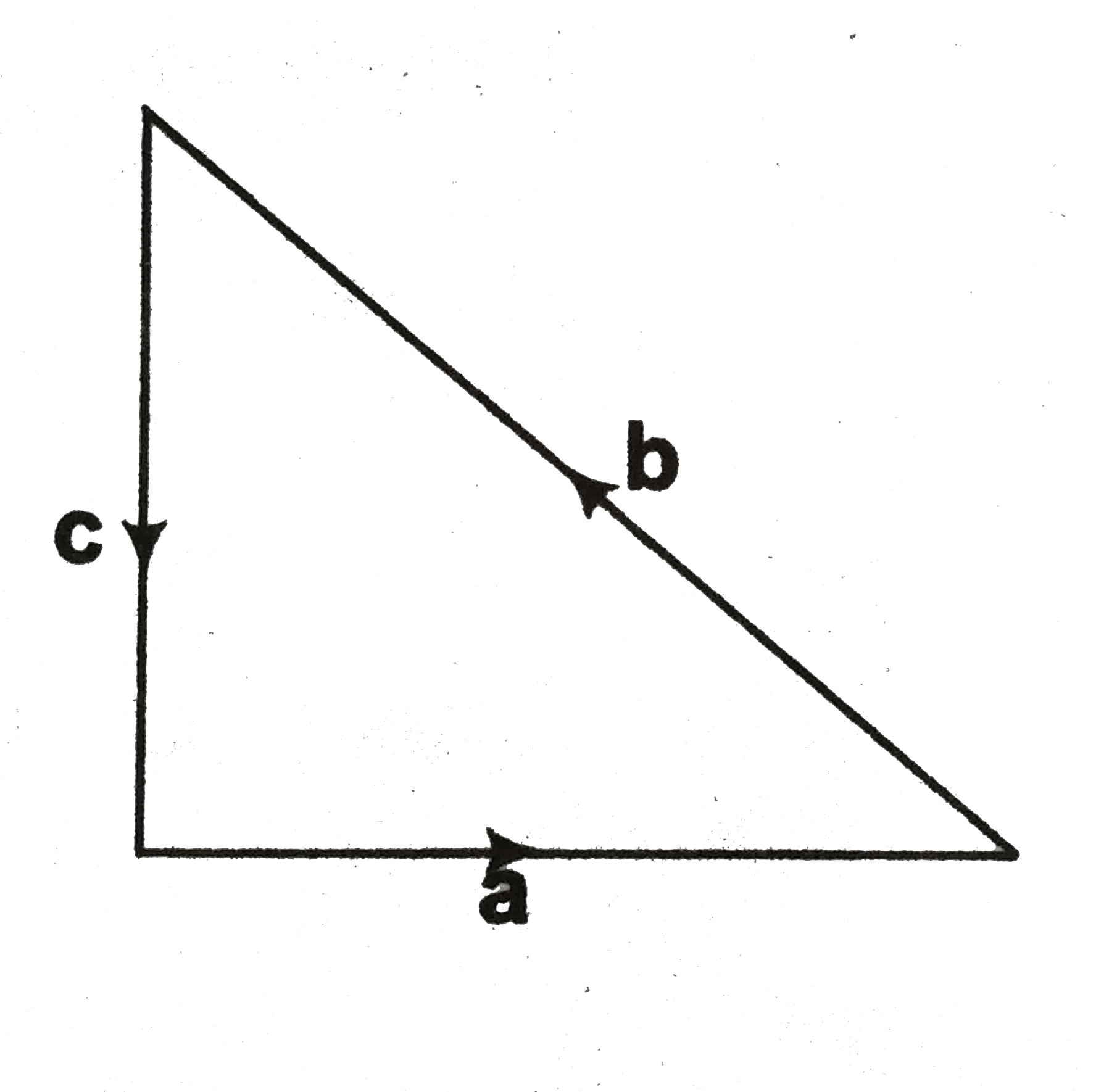
Show that the vectors $a = 3 ˆ i - 2 ˆ j + ˆ k, b = ˆ i - 3 ˆ j + 5 ˆ k$ and $c = 2 ˆ j + ˆ j - 4 ˆ k$ form a right angled triangle.

Video Solution

Text Solution

Verified by Experts

We have $b + c = (ˆ i - 3 ˆ j + 5 ˆ k) + (2 ˆ j + ˆ j - 4 ˆ k) = 3 ˆ i - 2 ˆ j + ˆ k = a$
Hence, a,b,c are coplanar.
Also, we observe that no two of theses vectors are parallel.
Further, $a . c = (3 ˆ i - 2 ˆ j + ˆ k) . (2 ˆ i + ˆ j - 4 ˆ k) = 0$
Dot product of two non-zero vectors is zero. Hence, they are perpendiuclar
so they form a right angled triangle.
$| a | = \sqrt{9 + 4 + 1} = \sqrt{14}$ ,
$| b | = \sqrt{1 + 9 + 25} = \sqrt{35}$
$| c | = \sqrt{4 + 1 + 16} = \sqrt{21}$
$\Rightarrow \sqrt{a^{2} + c^{2}} = {\sqrt{b}}^{2}$
.

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The three vectors $\to A = 3 ˆ i - 2 ˆ j + ˆ k, \to B = ˆ i - 3 ˆ j + 5 ˆ k$ and $\to C = 2 ˆ i + ˆ j - 4 ˆ k$ form
AAn equilateral triangle
BIsosceles triangle
CA right angled triangle
DNo triangle

DC PANDEY-VECTORS-Medical enrances gallery

Home
Ask Doubt
Profile