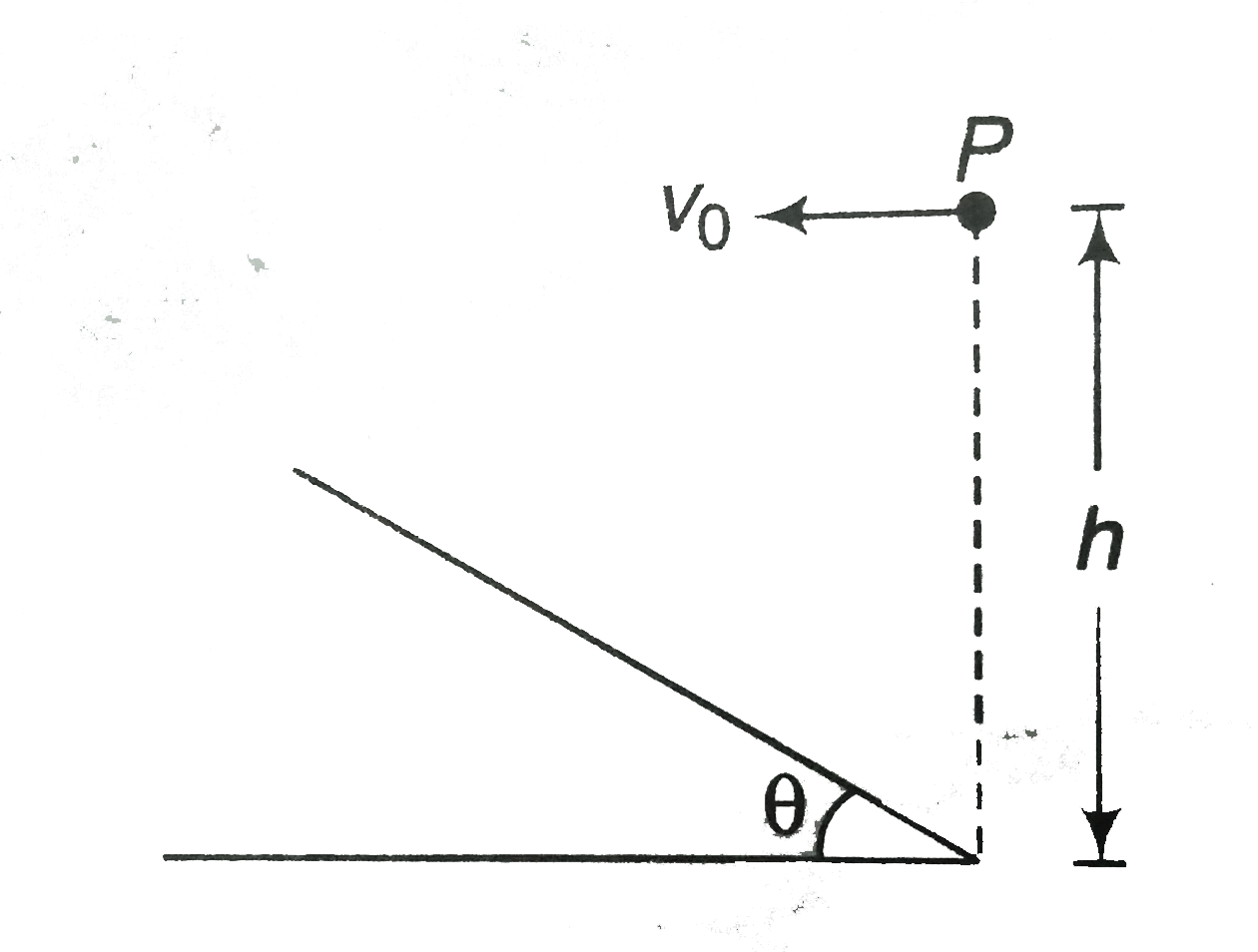
Determine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
The correct Answer is:A, B, C
ux=v0cosθ,uy=v0sinθ,ax=−gsinθ,
ay=gcosθ
At Q, vx=0
∴ux+axt=0

or t=v0cosθgsinθ ……..(i)
sy=hcosθ
∴uyt+12ayt2=hcosθ
∴(v0sinθ)(v0cosθgsinθ)
+12(gcosθ)(v0cosθgsinθ)=hcosθ
Solving this equation we get,
v0=√2gh2+cot2θ.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
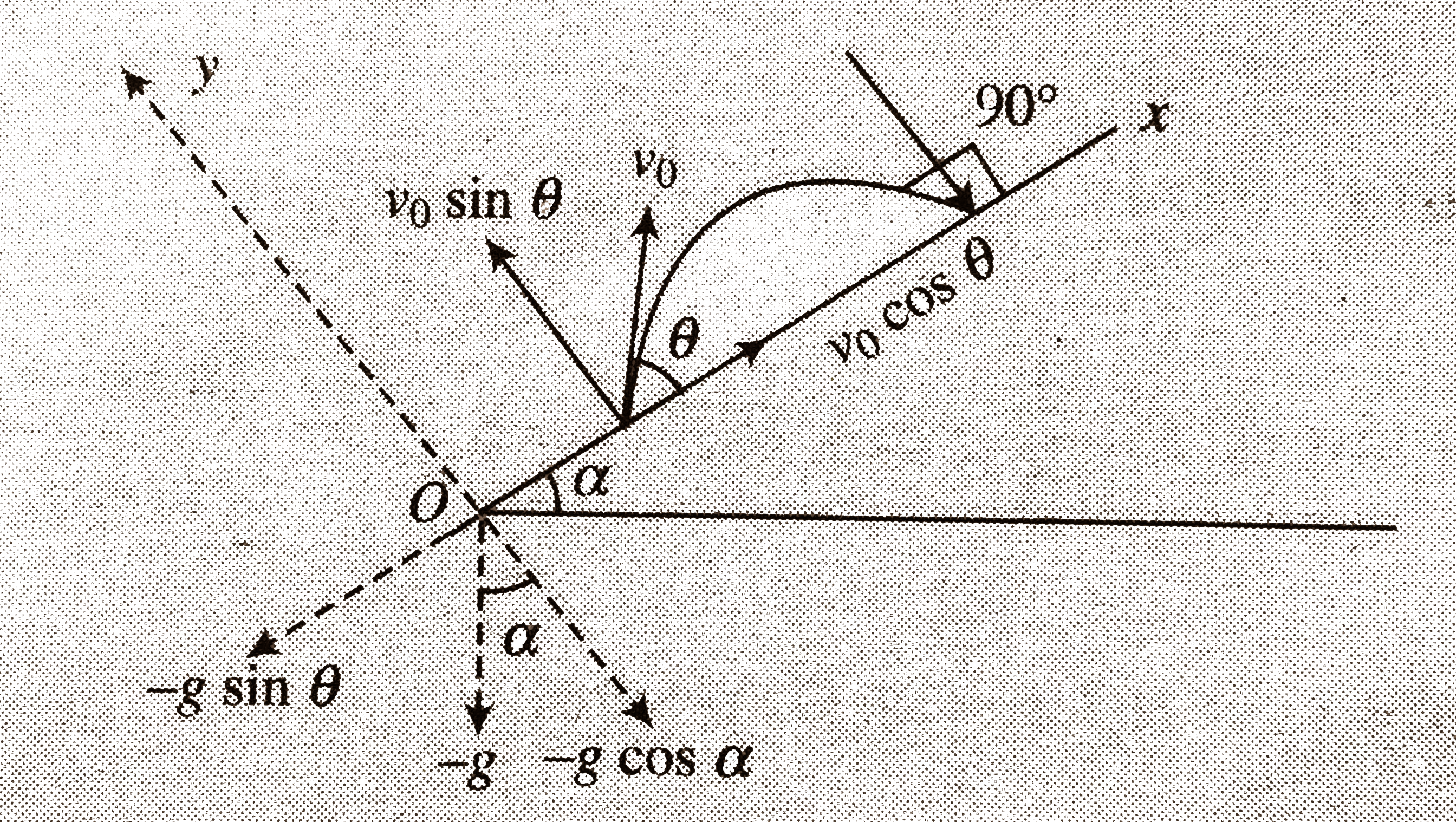
At what angle should a ball be projected up an inclined plane with a velocity v0 so that it may hir the incline normally. The angle of the inclined plane with the horozontal is ∝.
 .
.
View SolutionIn figure, find the horizontal velocity u(∈ms−1) of a projectile so that it hits the inclined plane perpendicularly. Given H=6.25m.

View Solution
Knowledge Check
In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . AV0=√2gH5BV0=√2gH7CV0=√gH5DV0=√gH7
. AV0=√2gH5BV0=√2gH7CV0=√gH5DV0=√gH7A particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
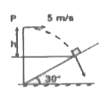 A3.75mB5.0mC4.75mD0.417m
A3.75mB5.0mC4.75mD0.417mThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
Agh1+k2/r2B2gh1+k2/r2C√gh1+k2/r2D√2gh1+k2/r2
A particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionA heavy block of length b and height h is placed at rest on a rough inclined plane of inclination θ with the horizontal, as shown in figure.

View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View Solution
