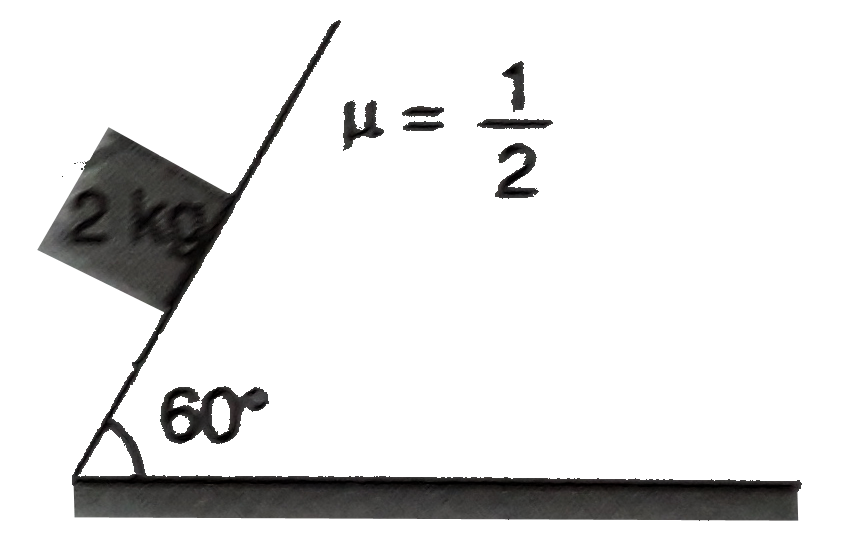
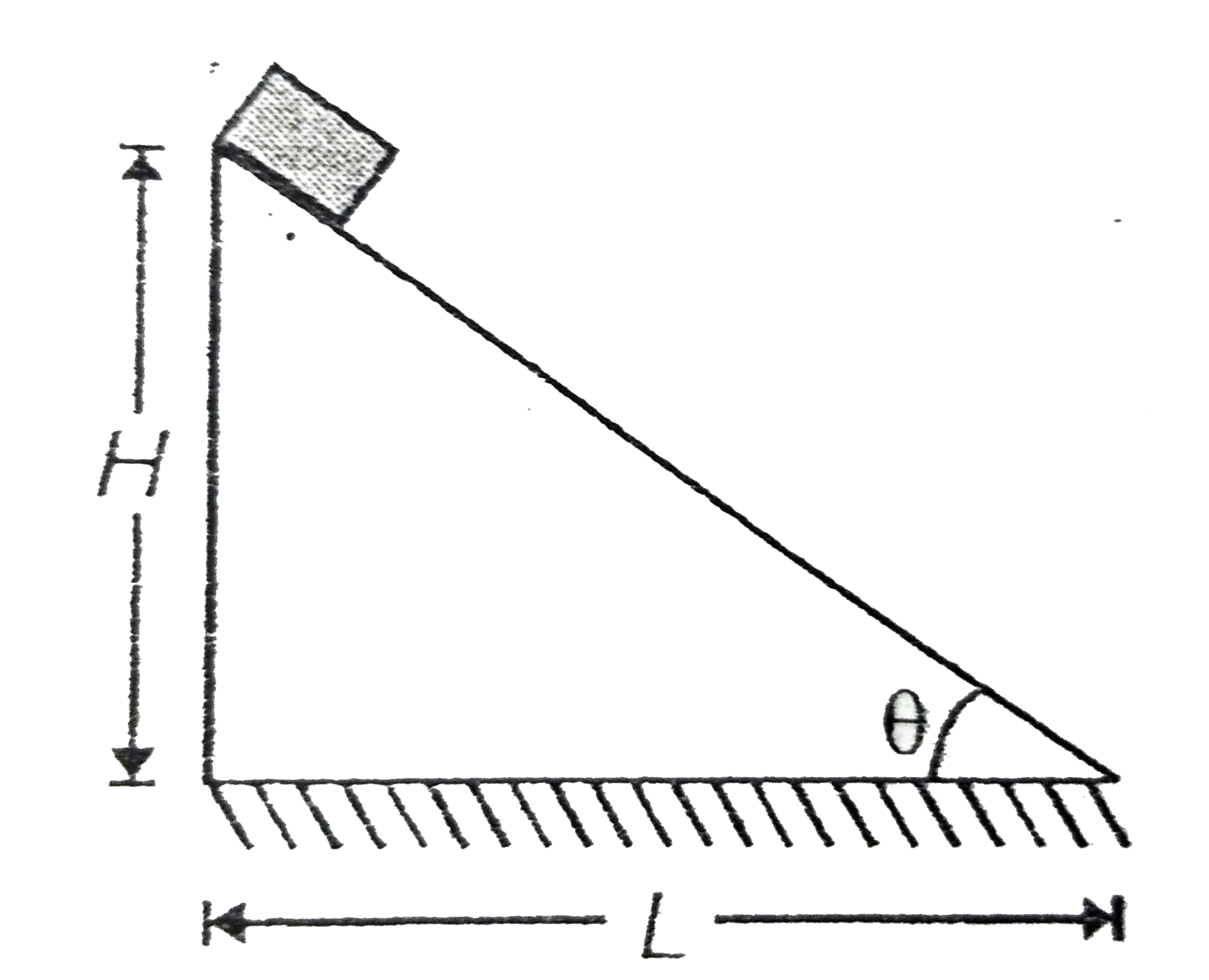
A block of mass 2kg is released from rest on a rough inclined ground as shown in figure. Find the work done on the block by.
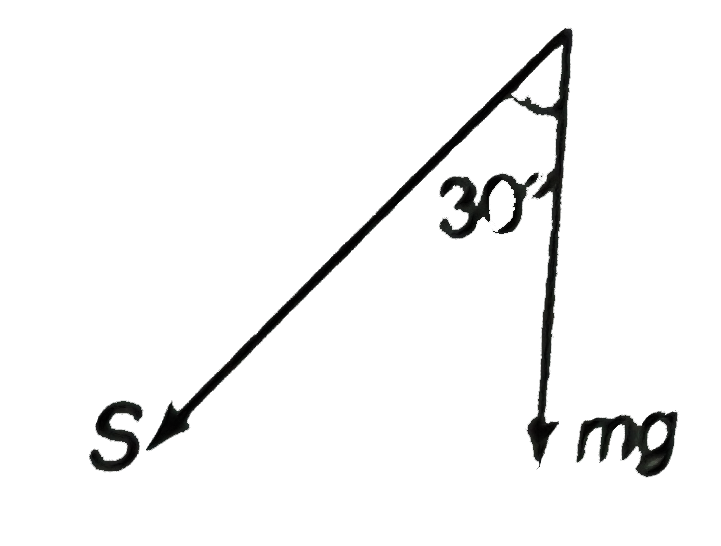
 .
.
(Take g10m/s2).
The correct Answer is:A, B, C, D
Wmg=(mg)(S)cos30∘
=(20)(2)(√3/2)
=34.6J
 .
.
(b) WfScos180∘
=(μmgcosθ)(S)(−1)

=−(12)(20)(cos60∘)(2)
=−10J.
Similar Questions
Knowledge Check
A block of mass 10 kg is released from top of rough inclined plane as shown in the figure if coefficient of friction between the block and inclined plane is then total work done on the block by all the forces acting on it till it reaches the bottom s = 10 ms
A200 jB300 jC100 jD-200 jA block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be
 A26NB19.5NC10ND30N
A26NB19.5NC10ND30N
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100M/m and block comes to rest after compressiong spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionTwo block of masses 2kg and 4kg are released from rest over a smooth inclined place of inclination 30∘ as shown in figure what is the normal force between the two blocks?

View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)

View Solution